Understanding Shapes

Q1: Multiple Choice Type

i. Finding the value of x + y + z + r is:

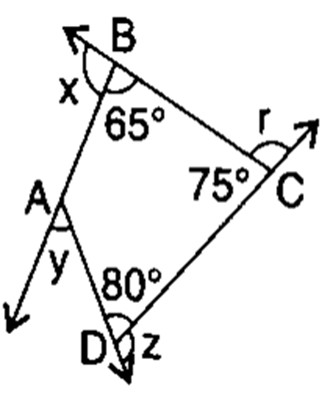
Step 1:At point B, angle x and 65° form a linear pair.
So, \[ x + 65° = 180°\\ x = 115° \]Step 2:At point A, angle y is vertically opposite to the interior angle between the two lines.
So, \[ y = 65° \]Step 3:At point D, angle z and 80° form a linear pair.
So, \[ z + 80° = 180°\\ z = 100° \]Step 4:At point C, angle r and 75° form a linear pair.
So, \[ r + 75° = 180°\\ r = 105° \]Step 5:Now add all the required angles: \[ x + y + z + r\\ = 115° + 65° + 100° + 105°\\ = 385° \]Step 6:Since these four angles are exterior angles taken around the figure, their sum equals one complete angle. \[ \text{Sum of exterior angles} = 360° \]Answer: c. 360°

ii. The angles of a quadrilateral are in the ratio 2 : 5 : 7 : 4. The largest angle is:

Step 1: Let the common ratio be \( k \). Then the angles are \( 2k, 5k, 7k, 4k \).
Step 2: The sum of interior angles of a quadrilateral is \( 360^\circ \). So, \[ 2k + 5k + 7k + 4k = 360^\circ \]Step 3: Simplify the equation: \[ 18k = 360^\circ \]Step 4: Find \( k \): \[ k = \frac{360^\circ}{18} = 20^\circ \]Step 5: The largest angle is \( 7k = 7 \times 20^\circ = 140^\circ \).
Answer: c. 140°

iii. In quadrilateral ABCD, ∠A = 45°, ∠B = 55° and ∠D = 60°; the quadrilateral is:

Step 1: The sum of interior angles of a quadrilateral is 360°. Find ∠C: \[ \angle C = 360^\circ – (45^\circ + 55^\circ + 60^\circ) = 360^\circ – 160^\circ = 200^\circ \] Step 2: Since ∠C = 200° > 180°, the quadrilateral has a reflex angle and is concave.
Answer: a. Concave

iv. In quadrilateral ABCD, ∠D = 40°, ∠C = 80°, AP bisects angle A and BP bisects angle ∠B; then ∠APB is equal:

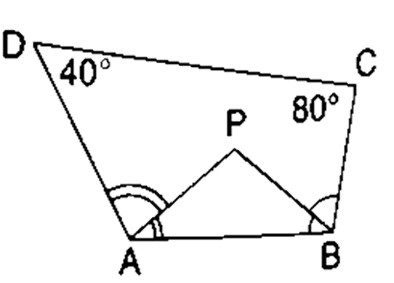
Step 1:Sum of interior angles of a quadrilateral is: \[ 360^\circ \]Step 2:Given: \[ \angle D = 40^\circ,\quad \angle C = 80^\circ \]So, \[ \angle A + \angle B = 360^\circ – (40^\circ + 80^\circ)\\ \angle A + \angle B = 360^\circ – 120^\circ = 240^\circ \]Step 3:AP bisects ∠A and BP bisects ∠B.
So, \[ \angle PAB = \frac{\angle A}{2}, \quad \angle PBA = \frac{\angle B}{2} \]Step 4:In triangle APB, sum of angles is 180°: \[ \angle APB + \frac{\angle A}{2} + \frac{\angle B}{2} = 180^\circ\\ \angle APB + \frac{\angle A + \angle B}{2} = 180^\circ \]Step 5:Substitute \(\angle A + \angle B = 240^\circ\): \[ \angle APB + \frac{240^\circ}{2} = 180^\circ\\ \angle APB + 120^\circ = 180^\circ\\ \angle APB = 60^\circ \]Answer: d. 60°

v. The sum of interior angles of a polygon is 900°. The number of sides in this polygon is:

Step 1: Formula for sum of interior angles of a polygon with \( n \) sides is: \[ (n – 2) \times 180^\circ = 900^\circ \]Step 2: Solve for \( n \): \[ (n – 2) = \frac{900^\circ}{180^\circ} = 5\\ n = 5 + 2 = 7 \]Answer: b. 7

Q2: Calculate the sum of angles of a polygon with 10 sides.

Step 1: Recall the formula for the sum of interior angles of a polygon with \( n \) sides: \[ \text{Sum of interior angles} = (n – 2) \times 180^\circ \]Step 2: Substitute \( n = 10 \) into the formula: \[ \text{Sum} = (10 – 2) \times 180^\circ \]Step 3: Simplify the expression: \[ = 8 \times 180^\circ = 1440^\circ \]Answer: The sum of interior angles of a polygon with 10 sides is 1440°.

Q3: Find the number of sides in a polygon if the sum of its interior angles is 16 right angles.

Step 1: Recall that 1 right angle = \(90^\circ\).
So, 16 right angles = \(16 \times 90^\circ = 1440^\circ\).
Step 2: Use the formula for sum of interior angles of a polygon with \( n \) sides: \[ (n – 2) \times 180^\circ = 1440^\circ \]Step 3: Solve for \( n \): \[ n – 2 = \frac{1440^\circ}{180^\circ} = 8\\ n = 8 + 2 = 10 \]Answer: The polygon has 10 sides.

Q4: Is it possible to have a polygon whose sum of interior angles is:

i. 870°

Step 1: Use the formula for sum of interior angles of a polygon with \( n \) sides: \[ (n – 2) \times 180^\circ = 870^\circ \]Step 2: Solve for \( n \): \[ n – 2 = \frac{870^\circ}{180^\circ} = 4.83\ldots \]Step 3: Since \( n \) is not an integer, a polygon cannot have sum of interior angles 870°.
Answer: Not possible.

ii. 2340°

Step 1: Use the formula: \[ (n – 2) \times 180^\circ = 2340^\circ \]Step 2: Solve for \( n \): \[ n – 2 = \frac{2340^\circ}{180^\circ} = 13\\ n = 13 + 2 = 15 \]Step 3: Since \( n \) is an integer, a polygon with 15 sides can have sum of interior angles 2340°.
Answer: Possible (15-sided polygon).

iii. 7 right angles

Step 1: Convert right angles to degrees: \[ 7 \times 90^\circ = 630^\circ \]Step 2: Use the formula: \[ (n – 2) \times 180^\circ = 630^\circ \]Step 3: Solve for \( n \): \[ n – 2 = \frac{630^\circ}{180^\circ} = 3.5 \]Step 4: Since \( n \) is not an integer, such a polygon is not possible.
Answer: Not possible.

Q5:

i. If all the angles of a hexagon are equal, find the measure of each angle.

Step 1: The sum of interior angles of a polygon with \( n \) sides is: \[ (n – 2) \times 180^\circ \]Step 2: For a hexagon, \( n = 6 \). So, sum of interior angles: \[ (6 – 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ \]Step 3: Since all angles are equal, each angle is: \[ \frac{720^\circ}{6} = 120^\circ \]Answer: Each angle of the hexagon measures 120°.

ii. If all the angles of a 14-sided figure are equal, find the measure of each angle.

Step 1: Use the formula for sum of interior angles: \[ (n – 2) \times 180^\circ \]Step 2: For \( n = 14 \): \[ (14 – 2) \times 180^\circ = 12 \times 180^\circ = 2160^\circ \]Step 3: Since all angles are equal, each angle is: \[ \frac{2160^\circ}{14} = \frac{1080^\circ}{7} = 154\frac{2}{7}^\circ \]Answer: Each angle of the 14-sided figure measures approximately \(154\frac{2}{7}^\circ\).

Q6: Find the sum of exterior angles obtained on producing the sides of a polygon, in order, with 7 sides.

Step 1: The sum of exterior angles of any polygon, when taken one at each vertex, is always \(360^\circ\), irrespective of the number of sides.
Step 2: Therefore, for a polygon with 7 sides, the sum of the exterior angles is: \(360^\circ\)
Answer: The sum of exterior angles of a 7-sided polygon is 360°.

Q7: The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are \( (6x – 1)^\circ \), \( (10x + 2)^\circ \), \( (8x + 2)^\circ \), \( (9x – 3)^\circ \), \( (5x + 4)^\circ \), and \( (12x + 6)^\circ \), find each exterior angle.

Step 1: The sum of exterior angles of any polygon is always \( 360^\circ \). So, \[ (6x – 1) + (10x + 2) + (8x + 2) + (9x – 3) + (5x + 4) + (12x + 6) = 360 \]Step 2: Combine like terms: \[ 6x + 10x + 8x + 9x + 5x + 12x + (-1 + 2 + 2 – 3 + 4 + 6) = 360\\ (6 + 10 + 8 + 9 + 5 + 12)x + ( -1 + 2 + 2 – 3 + 4 + 6 ) = 360\\ 50x + 10 = 360 \]Step 3: Solve for \( x \): \[ 50x = 360 – 10 = 350\\ x = \frac{350}{50} = 7 \]Step 4: Find each exterior angle by substituting \( x = 7 \) into the expressions: \[ 6x – 1 = 6 \times 7 – 1 = 42 – 1 = 41^\circ\\ 10x + 2 = 10 \times 7 + 2 = 70 + 2 = 72^\circ\\ 8x + 2 = 8 \times 7 + 2 = 56 + 2 = 58^\circ\\ 9x – 3 = 9 \times 7 – 3 = 63 – 3 = 60^\circ\\ 5x + 4 = 5 \times 7 + 4 = 35 + 4 = 39^\circ\\ 12x + 6 = 12 \times 7 + 6 = 84 + 6 = 90^\circ \]Answer: The exterior angles are 41°, 72°, 58°, 60°, 39°, and 90° respectively.

Q8: The interior angles of a pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Find each angle of the pentagon.

Step 1: Let the common ratio be \( k \). Then the angles are \( 4k, 5k, 6k, 7k, \) and \( 5k \).
Step 2: Sum of interior angles of a pentagon with \( n = 5 \) sides is: \[ (5 – 2) \times 180^\circ = 3 \times 180^\circ = 540^\circ \]Step 3: Sum of the angles in terms of \( k \): \[ 4k + 5k + 6k + 7k + 5k = 27k \]Step 4: Equate sum of angles to 540°: \[ 27k = 540^\circ \]Step 5: Solve for \( k \): \[ k = \frac{540^\circ}{27} = 20^\circ \]Step 6: Find each angle: \[ 4k = 4 \times 20^\circ = 80^\circ\\ 5k = 5 \times 20^\circ = 100^\circ\\ 6k = 6 \times 20^\circ = 120^\circ\\ 7k = 7 \times 20^\circ = 140^\circ\\ 5k = 5 \times 20^\circ = 100^\circ \]Answer: The interior angles of the pentagon are 80°, 100°, 120°, 140°, and 100° respectively.

Q9: Two angles of a hexagon are 120° and 160°. If the remaining four angles are equal, find each equal angle.

Step 1: The sum of interior angles of a hexagon (\( n = 6 \)) is: \[ (6 – 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ \]Step 2: Let each of the remaining four equal angles be \( x \) degrees. Then: \[ 120^\circ + 160^\circ + 4x = 720^\circ \]Step 3: Simplify and solve for \( x \): \[ 280^\circ + 4x = 720^\circ\\ 4x = 720^\circ – 280^\circ = 440^\circ\\ x = \frac{440^\circ}{4} = 110^\circ \]Answer: Each of the four equal angles measures 110°.

Q10: The figure given below shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B : ∠C : ∠D = 5 : 6 : 7.

i. Using formula, find the sum of interior angles of the pentagon

Step 1:Formula for sum of interior angles of a polygon with n sides: \[ (n – 2) \times 180^\circ \]Step 2:Here, number of sides \(n = 5\). \[ \text{Sum of interior angles} = (5 – 2) \times 180^\circ\\ = 3 \times 180^\circ\\ = 540^\circ \]Answer: Sum of interior angles of the pentagon = 540°

ii. Write the value of ∠A + ∠E

Step 1:Since AB ∥ ED, angles ∠A and ∠E are interior angles on the same side of a transversal.
Step 2:Interior angles on the same side of parallel lines are supplementary. \[ \angle A + \angle E = 180^\circ \]Answer: ∠A + ∠E = 180°

iii. Find angles B, C and D

Step 1:Sum of all interior angles of pentagon = 540°. \[ \angle A + \angle B + \angle C + \angle D + \angle E = 540^\circ \]Step 2:From part (ii): \[ \angle A + \angle E = 180^\circ \]So, \[ \angle B + \angle C + \angle D = 540^\circ – 180^\circ\\ = 360^\circ \]Step 3:Given ratio: \[ \angle B : \angle C : \angle D = 5 : 6 : 7 \]Let: \[ \angle B = 5x,\quad \angle C = 6x,\quad \angle D = 7x \]Step 4: \[ 5x + 6x + 7x = 360^\circ\\ 18x = 360^\circ\\ x = 20^\circ \]Step 5: \[ \angle B = 5 \times 20^\circ = 100^\circ\\ \angle C = 6 \times 20^\circ = 120^\circ\\ \angle D = 7 \times 20^\circ = 140^\circ \]Answer: ∠B = 100°, ∠C = 120°, ∠D = 140°

Q11: Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.

Step 1: Let the polygon have \( n \) sides. Then, it has 2 right angles and \( n – 2 \) angles of 120° each.
Step 2: The sum of interior angles of the polygon is: \[ 2 \times 90^\circ + (n – 2) \times 120^\circ \]Step 3: Use the formula for the sum of interior angles: \[ (n – 2) \times 180^\circ = 2 \times 90^\circ + (n – 2) \times 120^\circ \]Step 4: Simplify the equation: \[ 180n – 360 = 180 + 120n – 240\\ 180n – 360 = 120n – 60 \]Step 5: Bring all terms to one side: \[ 180n – 360 – 120n + 60 = 0\\ 60n – 300 = 0 \]Step 6: Solve for \( n \): \[ 60n = 300\\ n = \frac{300}{60} = 5 \]Answer: The polygon has 5 sides.

Q12: In a hexagon ABCDEF, side AB is parallel to side FE and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3. Find ∠B and ∠D.

Step 1: Calculate the sum of all interior angles of the hexagon.
Sum of angles = (n – 2) * 180°
For a hexagon, n = 6
Sum = (6 – 2) * 180° = 4 * 180° = 720°
∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°
Step 2: Use the property of parallel sides.
Since AB || FE, the sum of co-interior angles ∠A and ∠F is 180°.
∠A + ∠F = 180°
Step 3: Find the sum of the remaining angles.
∠B + ∠C + ∠D + ∠E = 720° – (∠A + ∠F)
∠B + ∠C + ∠D + ∠E = 720° – 180° = 540°
Step 4: Use the given ratio to find the angles.
Let the angles be 6k, 4k, 2k, and 3k.
6k + 4k + 2k + 3k = 540°
15k = 540°
k = 540° / 15 = 36°
Step 5: Calculate specific angles.
∠B = 6k = 6 * 36° = 216°
∠D = 2k = 2 * 36° = 72°
Answer: ∠B = 216° and ∠D = 72°.

Q13: The angles of a hexagon are \( x + 10^\circ \), \( 2x + 20^\circ \), \( 2x – 20^\circ \), \( 3x – 50^\circ \), \( x + 40^\circ \), and \( x + 20^\circ \). Find \( x \).

Step 1: The sum of interior angles of a hexagon (\( n=6 \)) is: \[ (6 – 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ \]Step 2: Sum of all given angles: \[ (x + 10) + (2x + 20) + (2x – 20) + (3x – 50) + (x + 40) + (x + 20) = 720 \]Step 3: Combine like terms: \[ x + 2x + 2x + 3x + x + x + 10 + 20 – 20 – 50 + 40 + 20 = 720\\ (1 + 2 + 2 + 3 + 1 + 1)x + (10 + 20 – 20 – 50 + 40 + 20) = 720\\ 10x + 20 = 720 \]Step 4: Solve for \( x \): \[ 10x = 720 – 20 = 700\\ x = \frac{700}{10} = 70 \]Answer: The value of \( x \) is 70.

Q14: In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3 : 7. Find the biggest angle of the pentagon.

Step 1: Sum of interior angles of a pentagon (\( n = 5 \)) is: \[ (5 – 2) \times 180^\circ = 3 \times 180^\circ = 540^\circ \]Step 2: Let the three remaining angles be \( k \), \( 3k \), and \( 7k \). Their sum is: \[ k + 3k + 7k = 11k \]Step 3: The sum of all angles: \[ 40^\circ + 60^\circ + 11k = 540^\circ \]Step 4: Solve for \( k \): \[ 100^\circ + 11k = 540^\circ\\ 11k = 540^\circ – 100^\circ = 440^\circ\\ k = \frac{440^\circ}{11} = 40^\circ \]Step 5: Find the three remaining angles: \[ k = 40^\circ, \quad 3k = 120^\circ, \quad 7k = 280^\circ \]Step 6: Identify the biggest angle: \[ \max(40^\circ, 60^\circ, 40^\circ, 120^\circ, 280^\circ) = 280^\circ \]Answer: The biggest angle of the pentagon is 280°.