Exercise: 3-B
Q1: Find the sum:
i. 16 + 21
→ Here, we are adding two positive numbers.
16 + 21 = 37
Answer: 37
ii. (–16) + 21
→ Here, we are adding a negative number and a positive number.
→ Since the absolute value of 21 is greater than that of –16, the result will be positive.
= 21 – 16 = 5
Answer: 5
iii. 16 + (–21)
→ Here, we are adding a positive number and a negative number.
→ Since the absolute value of 21 is greater than that of 16, the result will be negative.
= 16 – 21 = –5
Answer: –5
iv. (–25) + (–18)
→ Here, we are adding two negative numbers.
→ The result will be negative, and we add the absolute values.
= –(25 + 18) = –43
Answer: –43
v. (–32) + (–47)
→ Here, we are adding two negative numbers.
→ The result will be negative, and we add the absolute values.
= –(32 + 47) = –79
Answer: –79
vi. 54 + (–89)
→ Here, we are adding a positive number and a negative number.
→ Since the absolute value of 89 is greater than that of 54, the result will be negative.
= 54 – 89 = –35
Answer: –35
vii. (–38) + 45
→ Here, we are adding a negative number and a positive number.
→ Since the absolute value of 45 is greater than that of –38, the result will be positive.
= 45 – 38 = 7
Answer: 7
viii. 96 + (–103)
→ Here, we are adding a positive number and a negative number.
→ Since the absolute value of 103 is greater than that of 96, the result will be negative.
= 96 – 103 = –7
Answer: –7
ix. (–150) + (–15)
→ Here, we are adding two negative numbers.
→ The result will be negative, and we add the absolute values.
= –(150 + 15) = –165
Answer: –165
Q2: Write the additive inverse of:
i. 34
→ The additive inverse of a number is the number that, when added to the original number, gives zero.
→ The additive inverse of 34 is –34, because:
34 + (–34) = 0
Answer: –34
ii. –58
→ The additive inverse of –58 is 58, because:
–58 + 58 = 0
Answer: 58
iii. 0
→ The additive inverse of 0 is 0 itself, because:
0 + 0 = 0
Answer: 0
iv. –1
→ The additive inverse of –1 is 1, because:
–1 + 1 = 0
Answer: 1
v. 170
→ The additive inverse of 170 is –170, because:
170 + (–170) = 0
Answer: –170
Q3: Write the successor of:
i. 101
→ The successor of a number is the number that comes immediately after it.
→ The successor of 101 is 101 + 1 = 102
Answer: 102
ii. –47
→ The successor of a negative number is obtained by adding 1 to it.
→ The successor of –47 is –47 + 1 = –46
Answer: –46
iii. –1
→ The successor of –1 is –1 + 1 = 0
Answer: 0
iv. –80
→ The successor of –80 is –80 + 1 = –79
Answer: –79
v. –301
→ The successor of –301 is –301 + 1 = –300
Answer: –300
Q4: Write the predecessor of:
i. 40
→ The predecessor of a number is the number that comes immediately before it.
→ The predecessor of 40 is 40 – 1 = 39
Answer: 39
ii. –32
→ The predecessor of a negative number is obtained by subtracting 1 from it.
→ The predecessor of –32 is –32 – 1 = –33
Answer: –33
iii. –70
→ The predecessor of –70 is –70 – 1 = –71
Answer: –71
iv. –91
→ The predecessor of –91 is –91 – 1 = –92
Answer: –92
v. 0
→ The predecessor of 0 is 0 – 1 = –1
Answer: –1
Q5: Find the difference:
i. (15) – (21)
→ Subtracting a larger positive number from a smaller positive number results in a negative number.
→ 15 – 21 = –6
Answer: –6
ii. (-29) – (9)
→ Subtracting a positive number from a negative number makes the negative value more negative.
→ –29 – 9 = –38
Answer: –38
iii. 70 – (-8)
→ Subtracting a negative number is equivalent to adding the positive value.
→ 70 – (–8) = 70 + 8 = 78
Answer: 78
iv. 24 – (-24)
→ Subtracting a negative number is equivalent to adding the positive value.
→ 24 – (–24) = 24 + 24 = 48
Answer: 48
v. (-36) – (64)
→ Subtracting a positive number from a negative number makes the result more negative.
→ –36 – 64 = –100
Answer: –100
vi. 0 – (-20)
→ Subtracting a negative number is equivalent to adding the positive value.
→ 0 – (–20) = 0 + 20 = 20
Answer: 20
vii. (-63) – (-7)
→ Subtracting a negative number is equivalent to adding the positive value.
→ –63 – (–7) = –63 + 7 = –56
Answer: –56
viii. (-80) – (-20)
→ Subtracting a negative number is equivalent to adding the positive value.
→ –80 – (–20) = –80 + 20 = –60
Answer: –60
ix. (-12) – (-71)
→ Subtracting a negative number is equivalent to adding the positive value.
→ –12 – (–71) = –12 + 71 = 59
Answer: 59
Q6: Subtract:
i. -180 from 180
→ Subtracting a negative number is equivalent to adding the positive value.
→ 180 – (–180) = 180 + 180 = 360
Answer: 360
ii. 75 from -75
→ Subtracting a positive number from a negative number makes the result more negative.
→ –75 – 75 = –150
Answer: –150
iii. -630 from -70
→ Subtracting a positive number from a negative number makes the result more negative.
→ –70 – (–630) = –70 + 630 = 560
Answer: 560
iv. -95 from 0
→ Subtracting a negative number is equivalent to adding the positive value.
→ 0 – (–95) = 0 + 95 = 95
Answer: 95
v. -90 from -1
→ Subtracting a positive number from a negative number makes the result more negative.
→ –1 – (–90) = –1 + 90 = 89
Answer: 89
vi. -16 from -25
→ Subtracting a positive number from a negative number makes the result more negative.
→ –25 – (–16) = –25 + 16 = –9
Answer: –9
Q7: Fill in the blanks:
i. (+23) + ___ = 0
→ To make the sum zero, we need the opposite of 23.
→ (+23) + (–23) = 0
Answer: –23
ii. (-13) + ___ = 20
→ To make the sum 20, we need to add a number that, when added to 33, gives 20.
→ (–13) + (+33) = 20
Answer: +33
iii. (-14) + (___) = -34
→ To make the sum –34, we need to add a number that, when added to –14, gives –34.
→ –14 + (–20) = –34
Answer: –20
iv. (-20) + (___) = -8
→ To make the sum –8, we need to add a number that, when added to –20, gives –8.
→ –20 + 12 = –8
Answer: 12
v. (-30) – (___) = -14
→ To make the difference –14, we need to subtract a number from –30 that results in –14.
→ –30 – (–16) = –14
Answer: –16
vi. (___) -(-25) = 2
→ Subtracting a negative number is equivalent to adding the positive value.
→ (x) + 25 = 2
→ x = 2 – 25 = –23
Answer: –23
Q8: Use number line to find:
i. 5 + 4
→ Start from 5 and move 4 steps to the right.
→ The result is 9.
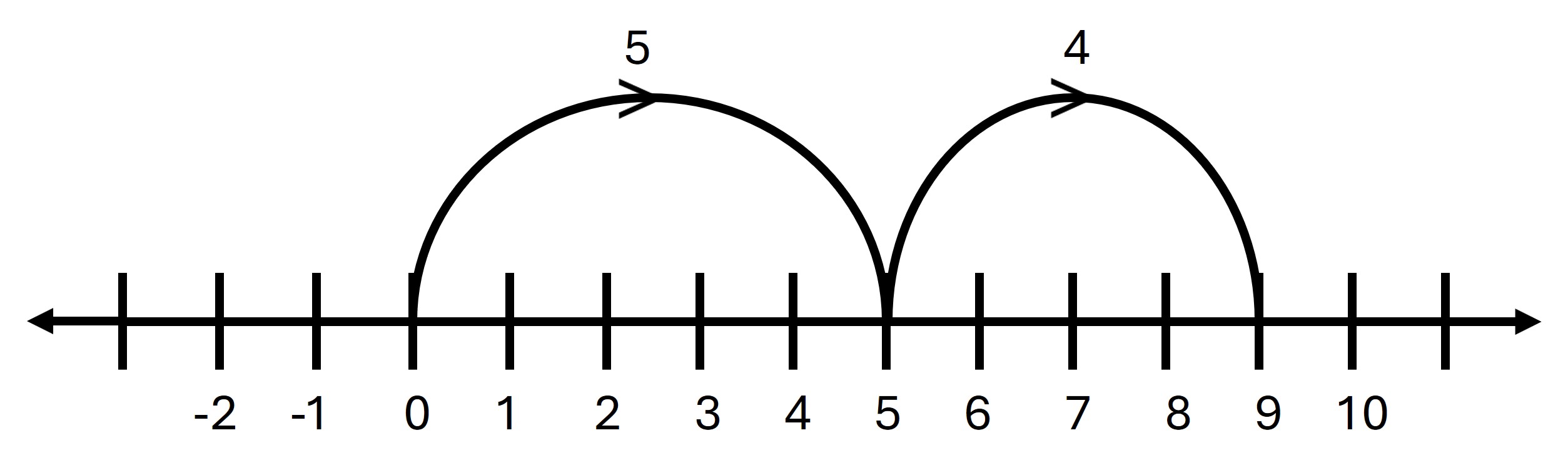
Answer: 9
ii. 4 + (-6)
→ Start from 4 and move 6 steps to the left.
→ The result is -2.
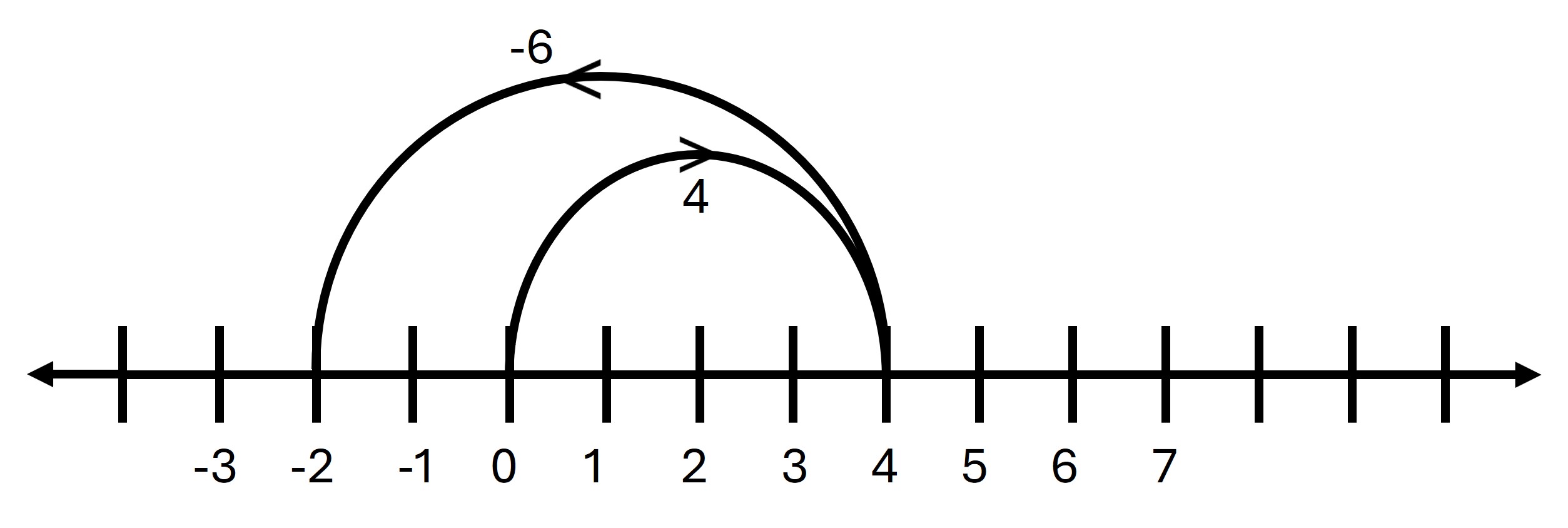
Answer: -2
iii. (-4) + 8
→ Start from -4 and move 8 steps to the right.
→ The result is 4.
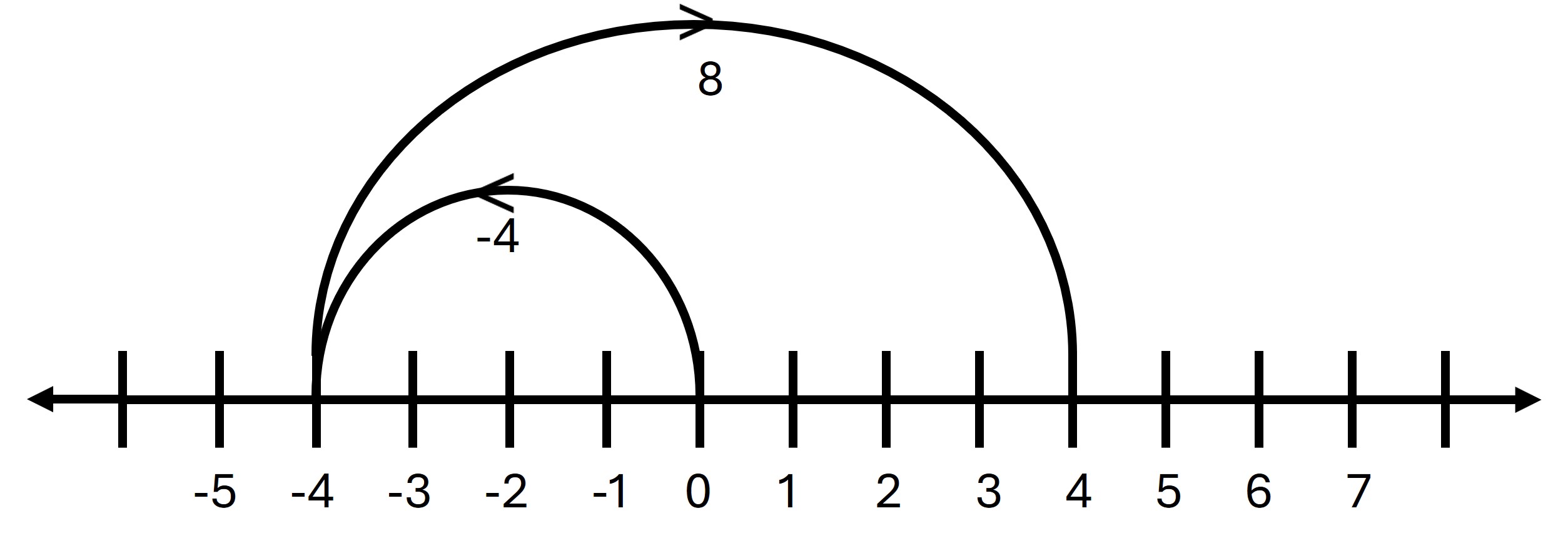
Answer: 4
iv. (-5) + 3
→ Start from -5 and move 3 steps to the right.
→ The result is -2.

Answer: -2
v. (-3) + (-5)
→ Start from -3 and move 5 steps to the left.
→ The result is -8.

Answer: -8
vi. (-6) + (-3)
→ Start from -6 and move 3 steps to the left.
→ The result is -9.
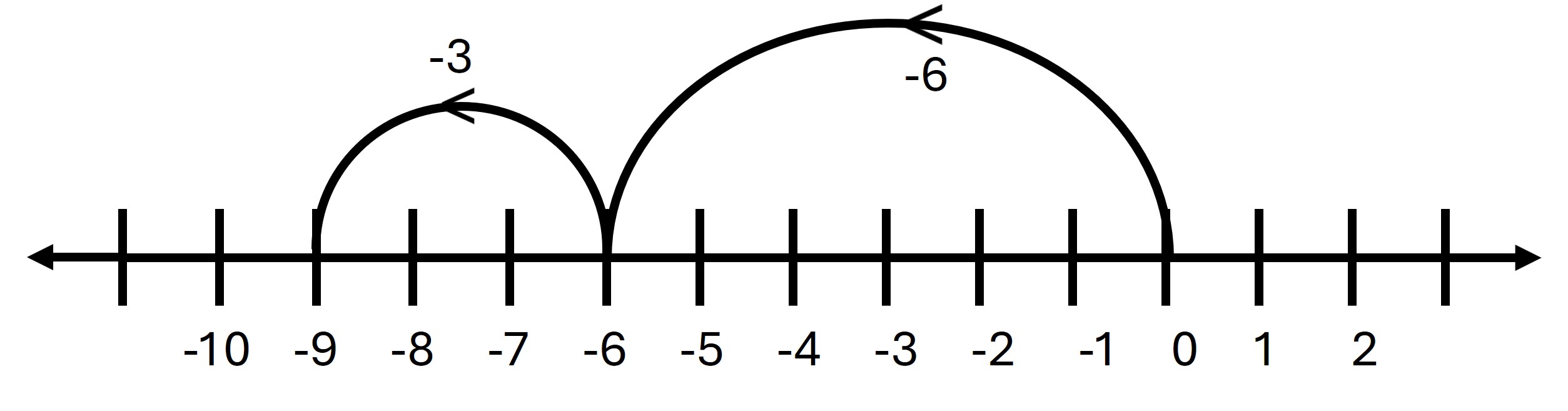
Answer: -9
vii. 5 – (-2)
→ Subtracting a negative number is the same as adding its positive counterpart.
→ 5 + 2 = 7
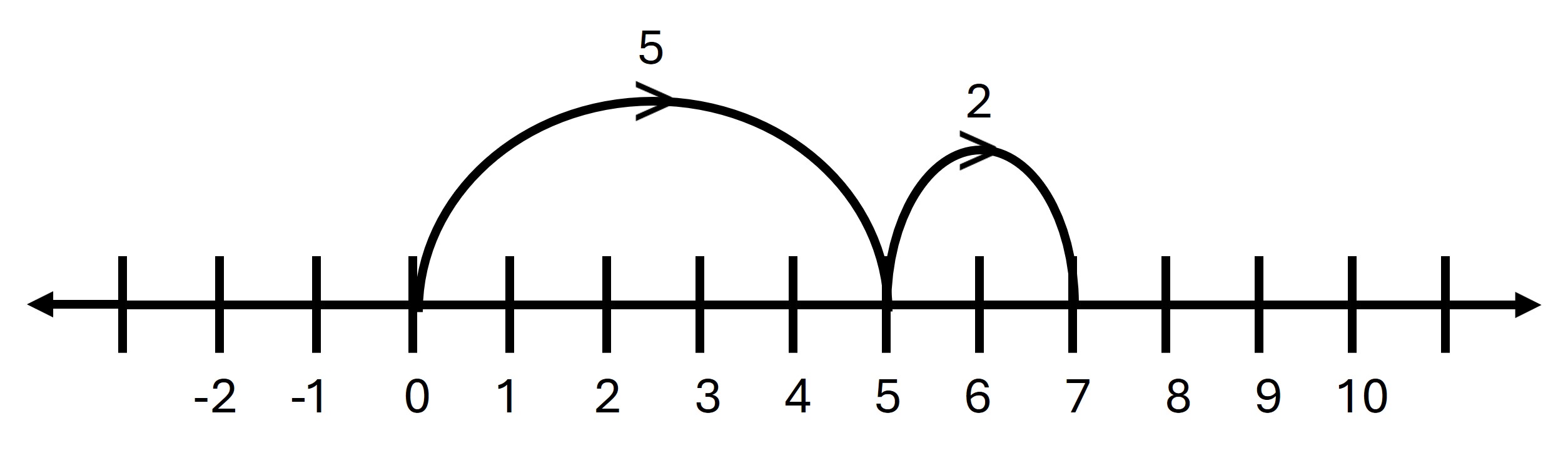
Answer: 7
viii. (-4) – 5
→ Start from -4 and move 5 steps to the left.
→ The result is -9.
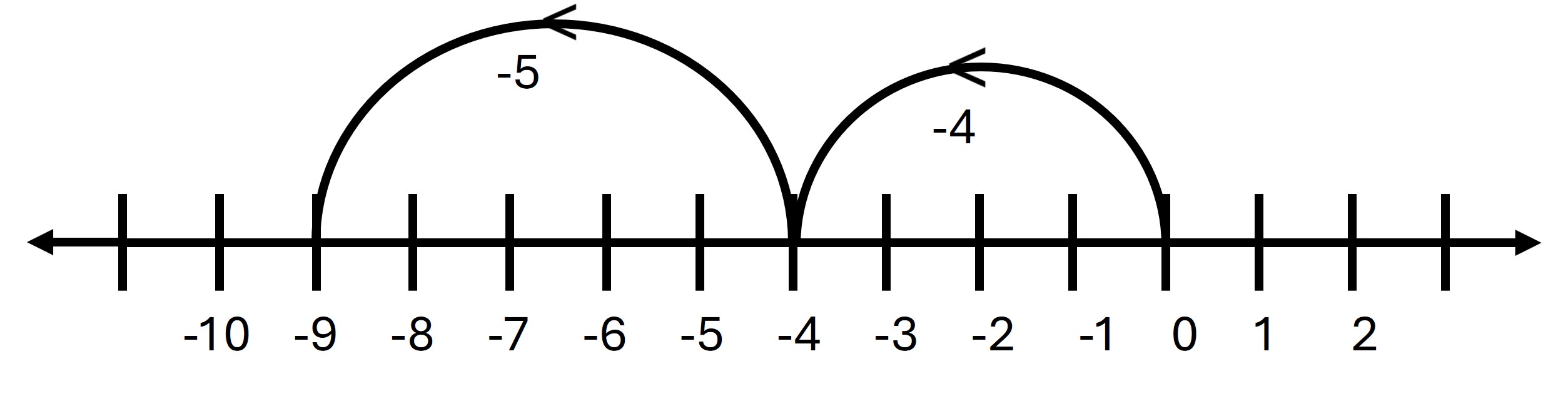
Answer: -9
ix. 4 – (-4)
→ Subtracting a negative number is the same as adding its positive counterpart.
→ 4 + 4 = 8
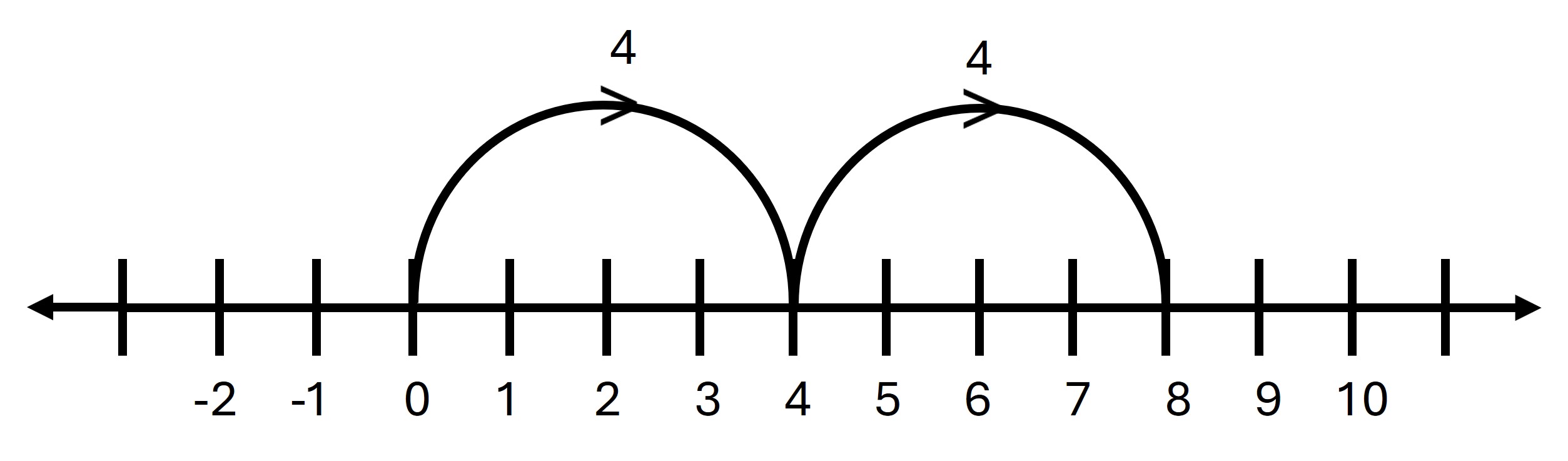
Answer: 8
Q9: State whether the given statement is true or false:
i. The sum of two integers is always an integer.
→ This statement is True.
→ The sum of any two integers, whether positive or negative, is always an integer.
Example: 3 + (-5) = -2.
ii. The difference of two integers is always an integer.
→ This statement is True.
→ The difference of any two integers is always an integer.
Example: 7 – 4 = 3.
iii. The absolute value of every integer is a positive integer.
→ This statement is False.
→ The absolute value of zero is zero, not a positive integer.
Example: |0| = 0 (not a positive integer).
iv. 0 is the smallest positive integer.
→ This statement is False.
→ Zero is neither positive nor negative. The smallest positive integer is 1.
v. Every whole number is an integer.
→ This statement is True.
→ Whole numbers are a subset of integers. Whole numbers include all non-negative integers (0, 1, 2, 3, …).
vi. The sum of two integers can never be zero.
→ This statement is False.
→ The sum of two integers can be zero when one is the additive inverse of the other.
Example: 5 + (-5) = 0.
Q10: What should be added to 15 to get (-15)?
We need to find the number x such that:
15 + x = -15
To isolate x, subtract 15 from both sides:
15 + x – 15 = -15 – 15
x = -15 – 15
x = -30
Therefore, the number that should be added to 15 to get (-15) is -30.
Q11: What should be subtracted from (-3) to get +18?
We need to find the number x such that:
(-3) – x = 18
To isolate x, add x to both sides and then add 3 to both sides:
(-3) – x + x = 18 + x
-x = 18 + 3
Now, simplify the right-hand side:
-x = 21
To get x, multiply both sides by -1:
x = -21
Therefore, the number that should be subtracted from (-3) to get +18 is -21.
Q12: The sum of two integers is -23. If one of them is 12, find the other.
We are given that the sum of two integers is -23. One of the integers is 12, and we are asked to find the other integer.
Let the unknown integer be represented by x.
We can express the relationship as:
12 + x = -23
To find the value of x, we need to isolate x on one side of the equation. To do this, subtract 12 from both sides of the equation:
12 + x – 12 = -23 – 12
This simplifies to:
x = -23 – 12
Now, we simplify the right-hand side:
x = -35
Therefore, the other integer is -35.
Q13: While playing children’s cards, Amit lost 70 points in the first game, 50 in the second game and 35 in the third game. He gained 60 in the fourth game and 80 in the fifth game. What was his net loss or gain?
To find the net loss or gain, we need to add up all the points that Amit lost and gained.
– Amit lost 70 points in the first game, 50 in the second game, and 35 in the third game. His total loss is:
Loss = -70 + (-50) + (-35)
– Amit gained 60 points in the fourth game and 80 in the fifth game. His total gain is:
Gain = +60 + (+80)
Now, we calculate the total loss and gain:
Total loss = -70 – 50 – 35 = -155
Total gain = 60 + 80 = +140
Now, to find the net result, we add the total gain to the total loss:
Net result = Total gain + Total loss = 140 + (-155)
Simplifying the equation:
Net result = 140 – 155 = -15
Therefore, Amit has a net loss of 15 points.
Q14: On one day on a hill, the temperature at 8 p.m. was 2°C but at mid-night that day, it fell down to -3°C. By how many degrees did the temperature fall?
We are given that the temperature at 8 p.m. was 2°C and at midnight, it fell to -3°C.
To find the change in temperature, we subtract the final temperature from the initial temperature:
Change in temperature = Initial temperature – Final temperature
Substituting the given values:
Change in temperature = 2°C – (-3°C)
Simplifying the equation:
Change in temperature = 2°C + 3°C
This gives us:
Change in temperature = 5°C
Therefore, the temperature fell by 5°C.
Q15: A car traveled east of Delhi by 100 km and then to the west of it by 130 km. How far from Delhi was the car finally?
The car traveled in two directions: first, it moved east by 100 km and then west by 130 km.
We need to find the car’s final distance from Delhi. To do this, we subtract the eastward distance from the westward distance.
Let the eastward distance be positive and the westward distance be negative.
Distance from Delhi = Eastward distance + Westward distance
Substituting the given values:
Distance from Delhi = +100 km + (-130 km)
Simplifying the equation:
Distance from Delhi = 100 – 130 = -30 km
The negative sign indicates that the car is 30 km to the west of Delhi.
Thus, the car is 30 km west of Delhi.






Leave a Comment