Exercise: 4-H
Q1: Represent \(\frac{2}{3}\) on the number line
Step 1: The denominator 3 means the whole is divided into 3 equal parts.
Step 2: The numerator 2 means we take 2 parts out of these 3 parts.
Step 3: On the number line from 0 to 1, divide the segment into 3 equal parts.
Step 4: Mark the point at the 2nd division which represents \(\frac{2}{3}\).
Answer: \(\frac{2}{3}\) lies between 0 and 1, exactly at the 2nd part when the segment from 0 to 1 is divided into 3 equal partS.
Number line from 0 to 1 divided into 3 equal parts:
0 1/3 2/3 1
|-------|--------|--------|
↑
2/3 here
Q2: Represent \(\frac{5}{8}\) on the number line
Step 1:
\(\frac{5}{8}\) means 5 parts out of 8 equal parts between 0 and 1.
Step 2:
Each part represents \(\frac{1}{8}\).
Step 3:
Starting from 0, count 5 parts to the right. This point is \(\frac{5}{8}\).
Number line:
0 1/8 2/8 3/8 4/8 5/8 6/8 7/8 1
|-----|-----|-----|-----|-----|-----|-----|-----|
↑
5/8 here
Q3: Represent \(\frac{1}{2}\) on the number line
Step 1:
\(\frac{1}{2}\) means 1 part out of 2 equal parts between 0 and 1.
Step 2:
Each part represents \(\frac{1}{2}\).
Step 3:
Starting from 0, count 1 part to the right. This point is \(\frac{1}{2}\).
Number line:
0 1/2 1
|----------|----------|
↑
1/2 here
Q4: Represent \(3\frac{3}{4}\) on the number line
Step 1:
\[
3\frac{3}{4} = \frac{3 \times 4 + 3}{4} = \frac{12 + 3}{4} = \frac{15}{4}
\]Step 2:
\(\frac{15}{4}\) means 15 parts each of \(\frac{1}{4}\).
Step 3:
Mark whole numbers 0, 1, 2, 3, 4… and divide each unit into 4 equal parts.
Since \(3\frac{3}{4} = 3 + \frac{3}{4}\), move 3 whole units and then 3 parts of \(\frac{1}{4}\) more.
Number line:
0 1 2 3 4
|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|-|
↑
3 3/4 here
Q5: Represent \(1\frac{4}{7}\) on the number line
Step 1:
\[
1\frac{4}{7} = \frac{1 \times 7 + 4}{7} = \frac{7 + 4}{7} = \frac{11}{7}
\]Step 2:
\(\frac{11}{7}\) means 11 parts each of \(\frac{1}{7}\).
Step 3: Mark whole numbers 0, 1, 2, … and divide each unit into 7 equal parts.
Since \(1\frac{4}{7} = 1 + \frac{4}{7}\), move 1 whole unit and then 4 parts of \(\frac{1}{7}\) more.
Number line:
0 1 2
|--|--|--|--|--|--|--|--|--|--|--|--|--|--|--|-
↑
1 4/7 here
Q6: Represent \(2\frac{2}{5}\) on the number line
Step 1:
\[
2\frac{2}{5} = \frac{2 \times 5 + 2}{5} = \frac{10 + 2}{5} = \frac{12}{5}
\]Step 2:
\(\frac{12}{5}\) means 12 parts each of \(\frac{1}{5}\).
Step 3:
Mark whole numbers 0, 1, 2, 3, … and divide each unit into 5 equal parts.
Since \(2\frac{2}{5} = 2 + \frac{2}{5}\), move 2 whole units and then 2 parts of \(\frac{1}{5}\) more.
Number line:
0 1 2 3
|--|--|--|--|--|--|--|--|--|--|--|--|--|--|--|-
↑
2 2/5 here
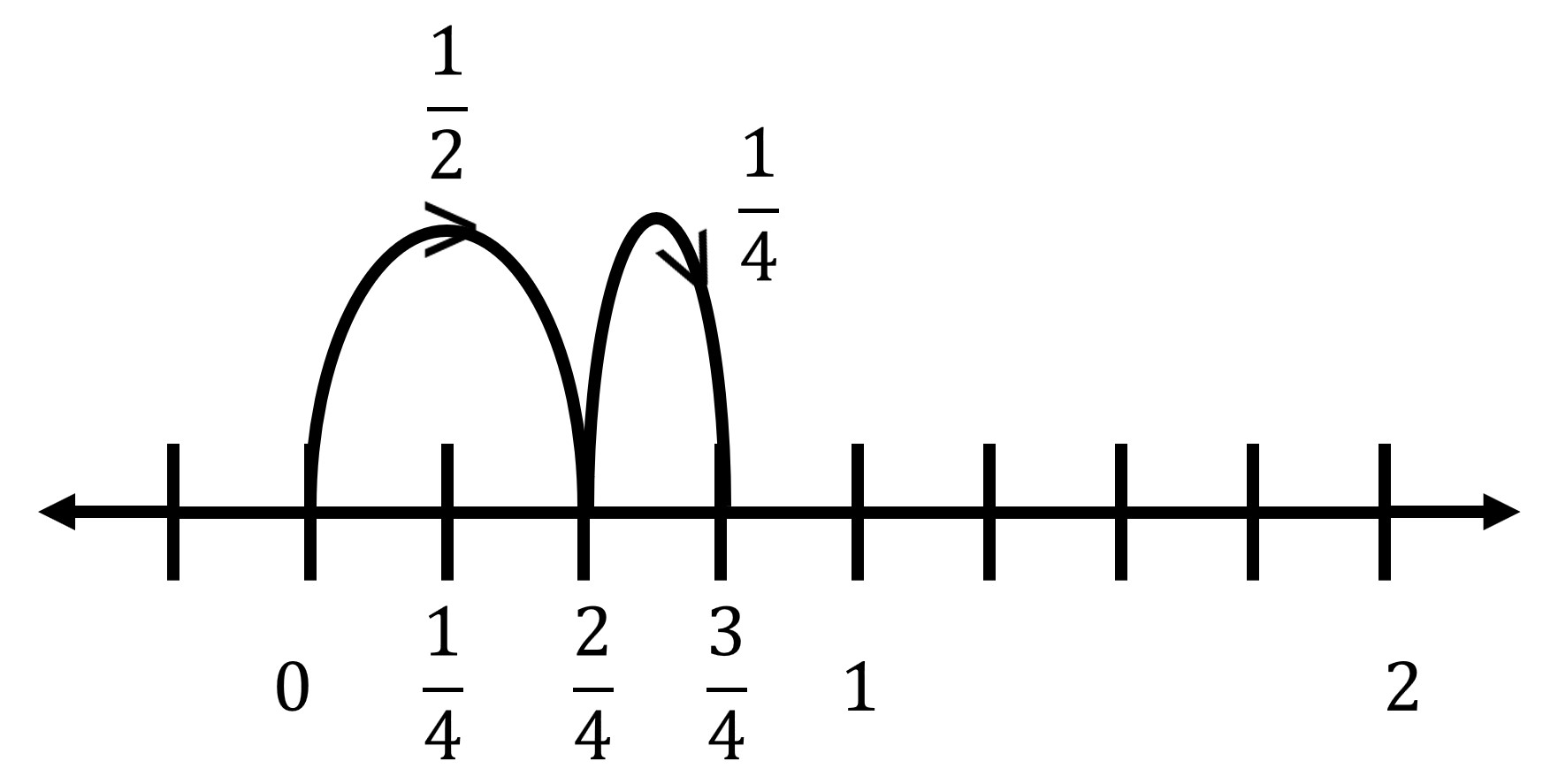
Q7: \(\frac{1}{2}+\frac{1}{4}\)
Step 1: Make denominators same (LCM of 2 and 4 is 4):
\[
\frac{1}{2} = \frac{2}{4}
\]Step 2:
\[
\frac{2}{4} + \frac{1}{4} = \frac{3}{4}
\]Step 3: Divide the interval from 0 to 1 into 4 equal parts and count 3 parts to mark \(\frac{3}{4}\).
Answer: \(\frac{3}{4}\)
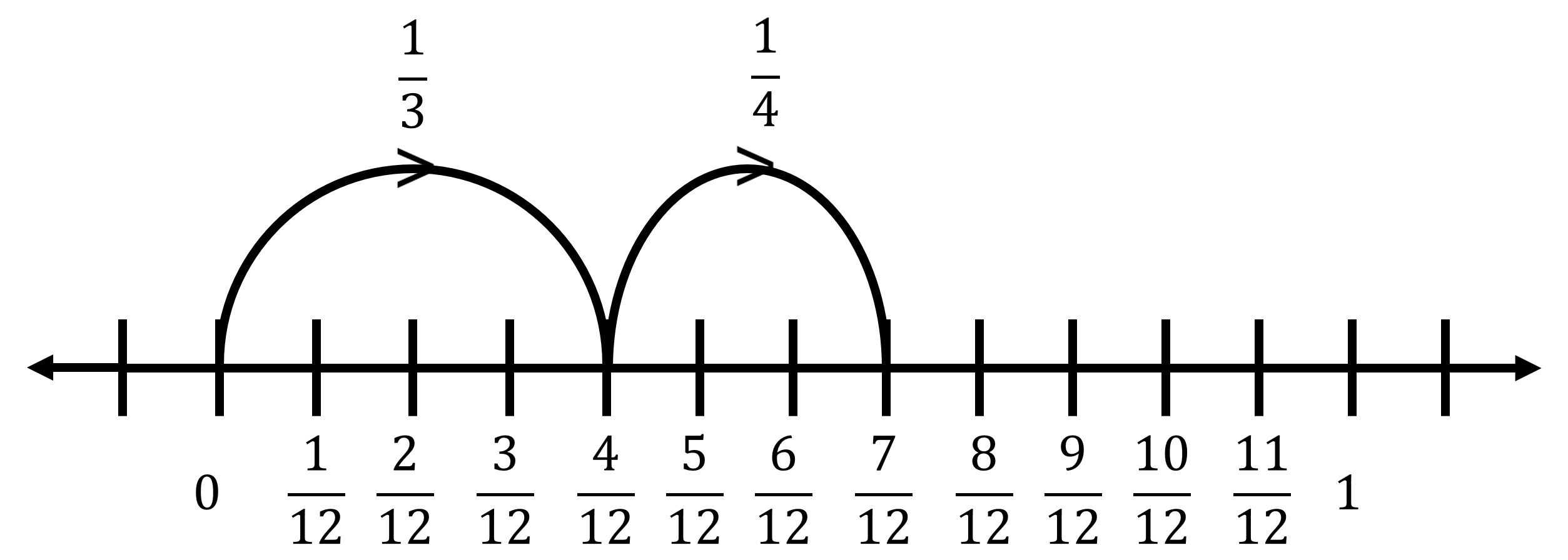
Q8: \(\frac{1}{3} + \frac{1}{4}\)
Step 1:
Find the LCM of the denominators 3 and 4.
\[
\text{LCM of 3 and 4} = 12
\]Step 2:
Convert both fractions to have the same denominator:
\[
\frac{1}{3} = \frac{4}{12}, \quad \frac{1}{4} = \frac{3}{12}
\]Step 3:
Add the converted fractions:
\[
\frac{4}{12} + \frac{3}{12} = \frac{7}{12}
\]Step 4:
Divide the number line from 0 to 1 into 12 equal parts and mark the 7th part to represent \(\frac{7}{12}\).
Answer: \(\frac{7}{12}\)
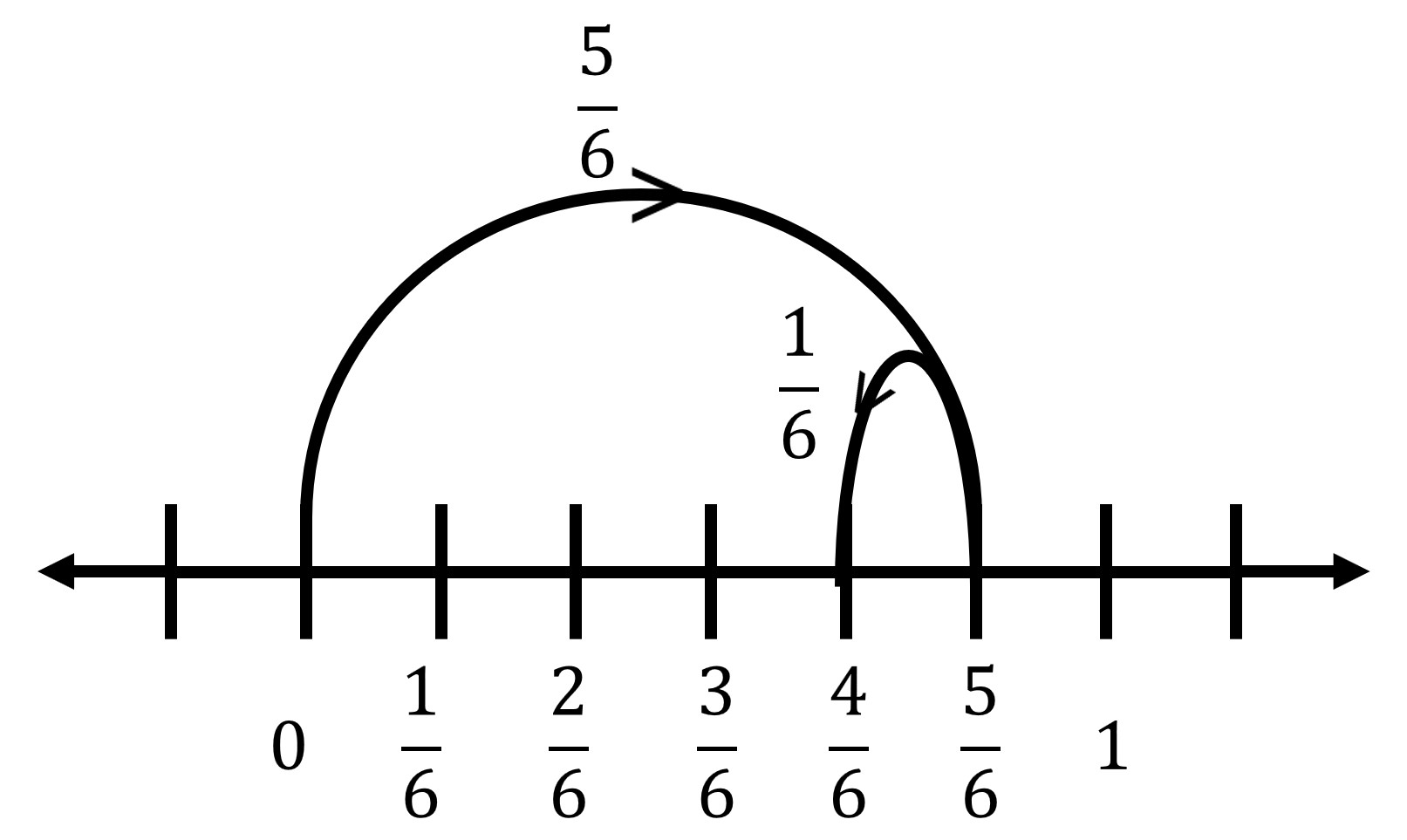
Q9: \(\frac{5}{6} – \frac{1}{6}\)
Step 1:
Both fractions have the same denominator:
\[
\frac{5}{6} – \frac{1}{6}
\]Step 2:
Subtract the numerators:
\[
\frac{5 – 1}{6} = \frac{4}{6}
\]Step 3:
Divide the number line from 0 to 1 into 6 equal parts and mark the 2nd part to represent \(\frac{4}{6}\).
Answer: \(\frac{2}{3}\)
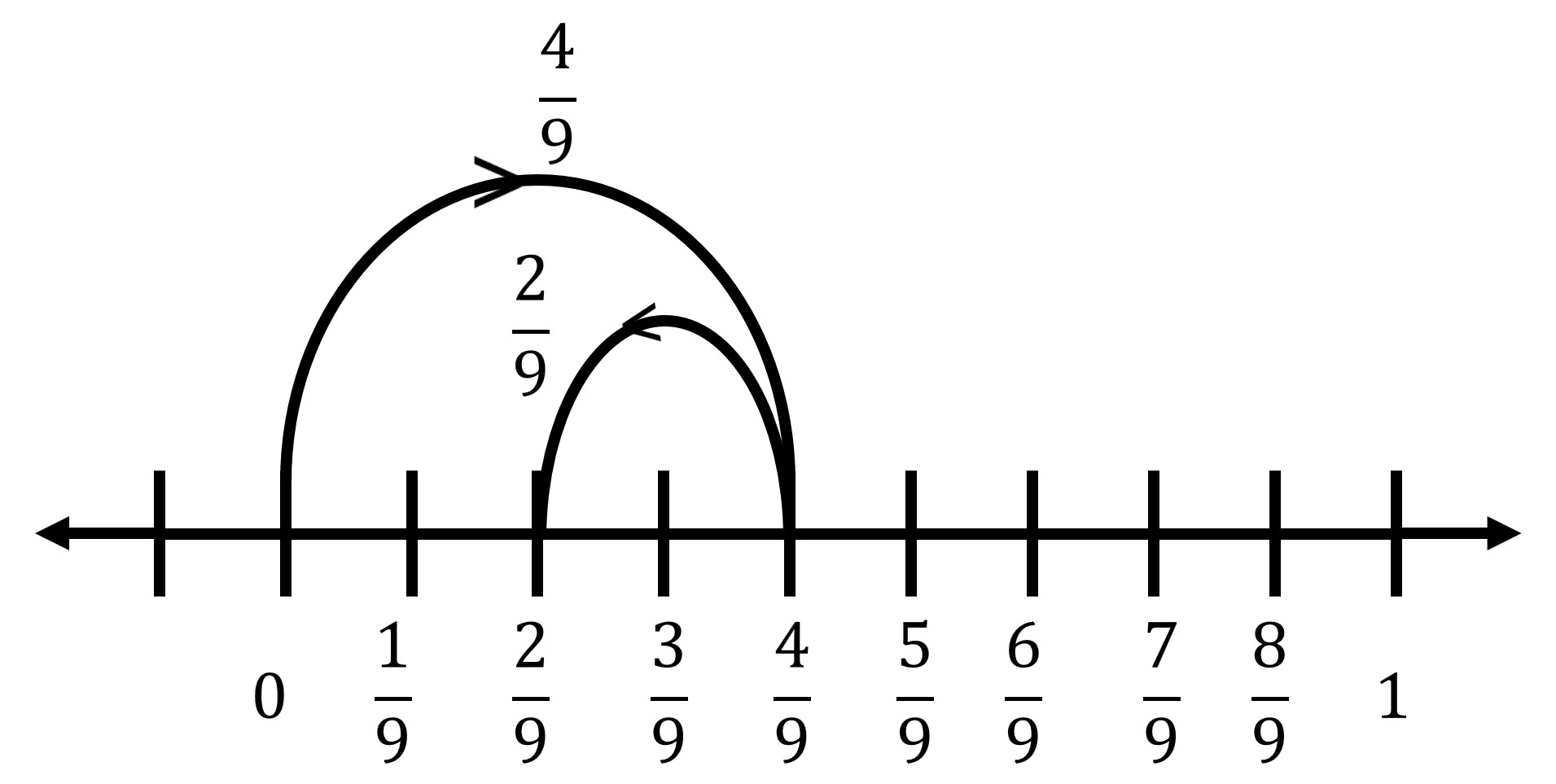
Q10: \(\frac{4}{9} – \frac{2}{9}\)
Step 1: Both fractions have the same denominator:
\[
\frac{4}{9} – \frac{2}{9}
\]Step 2: Subtract the numerators:
\[
\frac{4 – 2}{9} = \frac{2}{9}
\]Step 3: Divide the number line from 0 to 1 into 9 equal parts and mark the 2nd part to represent \(\frac{2}{9}\).
Answer: \(\frac{2}{9}\)






Leave a Comment