Fractions

Q1: What fractions do the shaded parts in each of the following figures represent?

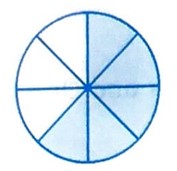
i. 5 parts out of 8 equal parts
Answer: \(\frac{5}{8}\)

ii. 7 parts out of 12 equal parts
Answer: \(\frac{7}{12}\)

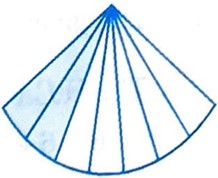
iii. 2 parts out of 7 equal parts
Answer: \(\frac{2}{7}\)

Q2: Write a fraction for each of the following:

i. 4 parts out of 9 equal parts

Step 1: “4 parts out of 9 equal parts” means 4 parts taken from a whole divided into 9 parts.
Step 2: The fraction is written as:
\(\frac{4}{9}\)
Answer: \(\frac{4}{9}\)

ii. 5 parts out of 11 equal parts

Step 1: “5 parts out of 11 equal parts” means a fraction with numerator 5 and denominator 11.
Step 2: So, the fraction is:
\(\frac{5}{11}\)
Answer: \(\frac{5}{11}\)

iii. two-fifths

Step 1: “Two-fifths” means 2 out of 5 equal parts.
Step 2: So, we write the fraction as:
\(\frac{2}{5}\)
Answer: \(\frac{2}{5}\)

iv. four-sevenths

Step 1: “Four-sevenths” represents 4 parts out of 7.
Step 2: Hence, the fraction is:
\(\frac{4}{7}\)
Answer: \(\frac{4}{7}\)

v. seven-tenths

Step 1: “Seven-tenths” means 7 out of 10 equal parts.
Step 2: The fraction becomes:
\(\frac{7}{10}\)
Answer: \(\frac{7}{10}\)

vi. six-eighths

Step 1: “Six-eighths” refers to 6 parts taken from 8 equal parts.
Step 2: So the fraction is:
\(\frac{6}{8}\)
Answer: \(\frac{6}{8}\)

Q3: Point out the numerator and denominator in each of the following fractions:

i. \(\frac{5}{6}\)

Step 1: In the fraction \(\frac{5}{6}\), the number above the line is the numerator and the number below the line is the denominator.
Step 2: Here, Numerator = 5, Denominator = 6
Answer: Numerator = 5, Denominator = 6

ii. \(\frac{3}{7}\)

Step 1: In the fraction \(\frac{3}{7}\), 3 is on the top and 7 is on the bottom.
Step 2: So, Numerator = 3, Denominator = 7
Answer: Numerator = 3, Denominator = 7

iii. \(\frac{9}{14}\)

Step 1: In \(\frac{9}{14}\), 9 is the number above the line → numerator, 14 is below the line → denominator.
Answer: Numerator = 9, Denominator = 14

iv. \(\frac{1}{20}\)

Step 1: In this fraction, 1 is on the top and 20 is on the bottom.
Step 2: So, Numerator = 1, Denominator = 20
Answer: Numerator = 1, Denominator = 20

v. \(\frac{12}{25}\)

Step 1: 12 is the numerator and 25 is the denominator in \(\frac{12}{25}\).
Answer: Numerator = 12, Denominator = 25

Q4: Write five fractions equivalent to each of the following:

i. \(\frac{2}{3}\)

Step 1: Multiply both numerator and denominator by the same number to get equivalent fractions.
Step 2: Multiply by 2, 3, 4, 5, 6 respectively:

• \(\frac{2×2}{3×2} = \frac{4}{6}\)
• \(\frac{2×3}{3×3} = \frac{6}{9}\)
• \(\frac{2×4}{3×4} = \frac{8}{12}\)
• \(\frac{2×5}{3×5} = \frac{10}{15}\)
• \(\frac{2×6}{3×6} = \frac{12}{18}\)

Answer: \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}, \frac{12}{18}\)

ii. \(\frac{3}{4}\)

Step 1: Multiply numerator and denominator by 2, 3, 4, 5, 6:

• \(\frac{3×2}{4×2} = \frac{6}{8}\)
• \(\frac{3×3}{4×3} = \frac{9}{12}\)
• \(\frac{3×4}{4×4} = \frac{12}{16}\)
• \(\frac{3×5}{4×5} = \frac{15}{20}\)
• \(\frac{3×6}{4×6} = \frac{18}{24}\)

Answer: \(\frac{6}{8}, \frac{9}{12}, \frac{12}{16}, \frac{15}{20}, \frac{18}{24}\)

iii. \(\frac{5}{6}\)

Step 1: Multiply both terms by 2, 3, 4, 5, 6:

• \(\frac{5×2}{6×2} = \frac{10}{12}\)
• \(\frac{5×3}{6×3} = \frac{15}{18}\)
• \(\frac{5×4}{6×4} = \frac{20}{24}\)
• \(\frac{5×5}{6×5} = \frac{25}{30}\)
• \(\frac{5×6}{6×6} = \frac{30}{36}\)

Answer: \(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}, \frac{25}{30}, \frac{30}{36}\)

iv. \(\frac{7}{9}\)

Step 1: Multiply numerator and denominator by 2 to 6:

• \(\frac{7×2}{9×2} = \frac{14}{18}\)
• \(\frac{7×3}{9×3} = \frac{21}{27}\)
• \(\frac{7×4}{9×4} = \frac{28}{36}\)
• \(\frac{7×5}{9×5} = \frac{35}{45}\)
• \(\frac{7×6}{9×6} = \frac{42}{54}\)

Answer: \(\frac{14}{18}, \frac{21}{27}, \frac{28}{36}, \frac{35}{45}, \frac{42}{54}\)

v. \(\frac{3}{14}\)

Step 1: Multiply numerator and denominator by 2 to 6:

• \(\frac{3×2}{14×2} = \frac{6}{28}\)
• \(\frac{3×3}{14×3} = \frac{9}{42}\)
• \(\frac{3×4}{14×4} = \frac{12}{56}\)
• \(\frac{3×5}{14×5} = \frac{15}{70}\)
• \(\frac{3×6}{14×6} = \frac{18}{84}\)

Answer: \(\frac{6}{28}, \frac{9}{42}, \frac{12}{56}, \frac{15}{70}, \frac{18}{84}\)

Q5: Which of the following are the pairs of equivalent fractions?

i. \(\frac{4}{5}\) and \(\frac{24}{30}\)

Step 1: Simplify \(\frac{24}{30}\):
\(\frac{24 \div 6}{30 \div 6} = \frac{4}{5}\)
Step 2: Both fractions become \(\frac{4}{5}\)
Answer: Equivalent

ii. \(\frac{6}{8}\) and \(\frac{18}{24}\)

Step 1: Simplify both fractions:
\(\frac{6}{8} = \frac{3}{4}\), \(\frac{18}{24} = \frac{3}{4}\)
Answer: Equivalent

iii. \(\frac{9}{16}\) and \(\frac{3}{4}\)

Step 1: Check if \(\frac{3}{4}\) can be written as \(\frac{9}{16}\)
\(\frac{3×4}{4×4} = \frac{12}{16} \ne \frac{9}{16}\)
Answer: Not Equivalent

iv. \(\frac{8}{12}\) and \(\frac{14}{21}\)

Step 1: Simplify both:
\(\frac{8}{12} = \frac{2}{3}\), \(\frac{14}{21} = \frac{2}{3}\)
Answer: Equivalent

v. \(\frac{7}{11}\) and \(\frac{21}{32}\)

Step 1: Check cross-multiplication:
\(7 × 32 = 224\), \(11 × 21 = 231\)
\(224 \ne 231\)
Answer: Not Equivalent

vi. \(\frac{5}{12}\) and \(\frac{35}{84}\)

Step 1: Simplify \(\frac{35}{85}\):
\(\frac{35}{84} = \frac{5}{12}\)
Step 2: Both fractions become \(\frac{5}{12}\)
Answer: Equivalent

Q6: Write an equivalent fraction of:

i. \(\frac{4}{5}\) with numerator 32

Step 1: To find the multiplier, divide the required numerator by the original numerator:
\[ \frac{32}{4} = 8 \] Step 2: Multiply both numerator and denominator by 8: \[ \frac{4 \times 8}{5 \times 8} = \frac{32}{40} \] Answer: \(\frac{32}{40}\)

ii. \(\frac{7}{9}\) with numerator 42

Step 1: Find the multiplier: \[ \frac{42}{7} = 6 \] Step 2: Multiply numerator and denominator by 6: \[ \frac{7 \times 6}{9 \times 6} = \frac{42}{54} \] Answer: \(\frac{42}{54}\)

iii. \(\frac{3}{7}\) with denominator 63

Step 1: Find the multiplier for denominator: \[ \frac{63}{7} = 9 \] Step 2: Multiply both terms by 9: \[ \frac{3 \times 9}{7 \times 9} = \frac{27}{63} \] Answer: \(\frac{27}{63}\)

iv. \(\frac{10}{13}\) with denominator 78

Step 1: Find the multiplier for denominator: \[ \frac{78}{13} = 6 \] Step 2: Multiply both terms by 6: \[ \frac{10 \times 6}{13 \times 6} = \frac{60}{78} \] Answer: \(\frac{60}{78}\)

Q7: Write an equivalent fraction of:

i. \(\frac{32}{48}\) with numerator 2

Step 1: Find the factor by which the numerator 32 is reduced to 2: \[ \frac{32}{2} = 16 \] Step 2: Divide both numerator and denominator by 16: \[ \frac{32 \div 16}{48 \div 16} = \frac{2}{3} \] Answer: \(\frac{2}{3}\)

ii. \(\frac{21}{28}\) with numerator 3

Step 1: Find the factor: \[ \frac{21}{3} = 7 \] Step 2: Divide both terms by 7: \[ \frac{21 \div 7}{28 \div 7} = \frac{3}{4} \] Answer: \(\frac{3}{4}\)

iii. \(\frac{24}{56}\) with denominator 7

Step 1: Find the factor to reduce the denominator from 56 to 7: \[ \frac{56}{7} = 8 \] Step 2: Divide both terms by 8: \[ \frac{24 \div 8}{56 \div 8} = \frac{3}{7} \] Answer: \(\frac{3}{7}\)

iv. \(\frac{121}{132}\) with denominator 12

Step 1: Find the factor to reduce the denominator: \[ \frac{132}{12} = 11 \] Step 2: Divide both terms by 11: \[ \frac{121 \div 11}{132 \div 11} = \frac{11}{12} \] Answer: \(\frac{11}{12}\)

Q8: Write an equivalent fraction of:

i. \(\frac{45}{54}\) with numerator 20

Step 1: Find the factor to scale down the numerator from 45 to 20:
\[ \frac{45}{20} = \frac{9}{4} \quad \Rightarrow \quad \text{Not a whole number (impractical to use directly)} \] Step 2: Instead, reduce the original fraction first:
\[ \frac{45 \div 9}{54 \div 9} = \frac{5}{6} \] Step 3: Find the factor to scale numerator 5 to 20: \[ \frac{20}{5} = 4 \] Step 4: Multiply both numerator and denominator by 4: \[ \frac{5 \times 4}{6 \times 4} = \frac{20}{24} \] Answer: \(\frac{20}{24}\)

ii. \(\frac{75}{90}\) with denominator 42

Step 1: Simplify the original fraction first: \[ \frac{75 \div 15}{90 \div 15} = \frac{5}{6} \] Step 2: Find the factor to convert denominator 6 to 42: \[ \frac{42}{6} = 7 \] Step 3: Multiply both numerator and denominator by 7: \[ \frac{5 \times 7}{6 \times 7} = \frac{35}{42} \] Answer: \(\frac{35}{42}\)

Q9: Write the missing numerals in the place-holders:

i. \(\frac{4}{9} = \frac{}{63}\)

Step 1: Find the factor from 9 to 63:
\[ \frac{63}{9} = 7 \] Step 2: Multiply the numerator by 7: \[ 4 \times 7 = 28 \] Answer: \(\frac{4}{9} = \frac{28}{63}\)

ii. \(\frac{3}{4} = \frac{18}{}\)

Step 1: Find the factor from 3 to 18:
\[ \frac{18}{3} = 6 \] Step 2: Multiply the denominator by 6: \[ 4 \times 6 = 24 \] Answer: \(\frac{3}{4} = \frac{18}{24}\)

iii. \(\frac{42}{70} = \frac{3}{}\)

Step 1: Reduce \(\frac{42}{70}\) to lowest terms: \[ \frac{42 \div 14}{70 \div 14} = \frac{3}{5} \] Step 2: So, denominator is: 5
Answer: \(\frac{42}{70} = \frac{3}{5}\)

iv. \(\frac{52}{78} = \frac{}{6}\)

Step 1: Reduce \(\frac{52}{78}\) to lowest terms:
Find HCF of 52 and 78 = 26
\[ \frac{52 \div 26}{78 \div 26} = \frac{2}{3} \] Step 2: Find factor to convert 3 to 6: \[ \frac{6}{3} = 2 \] Step 3: Multiply numerator by 2: \[ 2 \times 2 = 4 \] Answer: \(\frac{52}{78} = \frac{4}{6}\)

Q10: What fraction of an hour is 25 minutes?

Step 1: We know that 1 hour = 60 minutes.
Step 2: So, 25 minutes out of 60 minutes is written as a fraction:
\[ \frac{25}{60} \]Step 3: Simplify the fraction by dividing both numerator and denominator by 5:
\[ \frac{25 \div 5}{60 \div 5} = \frac{5}{12} \]Answer: \(\frac{5}{12}\) of an hour

Q11: What fraction of a day is 9 hours?

Step 1: We know that 1 day = 24 hours.
Step 2: So, 9 hours out of 24 hours is written as a fraction:
\[ \frac{9}{24} \]Step 3: Simplify the fraction by dividing both numerator and denominator by 3:
\[ \frac{9 \div 3}{24 \div 3} = \frac{3}{8} \]Answer: \(\frac{3}{8}\) of a day