Exercise: 16-A
Q1: Multiple Choice Type
i. Finding the value of x + y + z + r is:
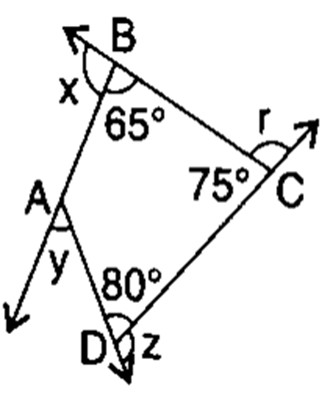
Step 1:At point B, angle x and 65° form a linear pair.
So,
\[
x + 65° = 180°\\
x = 115°
\]Step 2:At point A, angle y is vertically opposite to the interior angle between the two lines.
So,
\[
y = 65°
\]Step 3:At point D, angle z and 80° form a linear pair.
So,
\[
z + 80° = 180°\\
z = 100°
\]Step 4:At point C, angle r and 75° form a linear pair.
So,
\[
r + 75° = 180°\\
r = 105°
\]Step 5:Now add all the required angles:
\[
x + y + z + r\\
= 115° + 65° + 100° + 105°\\
= 385°
\]Step 6:Since these four angles are exterior angles taken around the figure, their sum equals one complete angle.
\[
\text{Sum of exterior angles} = 360°
\]Answer: c. 360°
ii. The angles of a quadrilateral are in the ratio 2 : 5 : 7 : 4. The largest angle is:
Step 1: Let the common ratio be \( k \). Then the angles are \( 2k, 5k, 7k, 4k \).
Step 2: The sum of interior angles of a quadrilateral is \( 360^\circ \). So,
\[
2k + 5k + 7k + 4k = 360^\circ
\]Step 3: Simplify the equation:
\[
18k = 360^\circ
\]Step 4: Find \( k \):
\[
k = \frac{360^\circ}{18} = 20^\circ
\]Step 5: The largest angle is \( 7k = 7 \times 20^\circ = 140^\circ \).
Answer: c. 140°
iii. In quadrilateral ABCD, ∠A = 45°, ∠B = 55° and ∠D = 60°; the quadrilateral is:
Step 1: The sum of interior angles of a quadrilateral is 360°. Find ∠C:
\[
\angle C = 360^\circ – (45^\circ + 55^\circ + 60^\circ) = 360^\circ – 160^\circ = 200^\circ
\]
Step 2: Since ∠C = 200° > 180°, the quadrilateral has a reflex angle and is concave.
Answer: a. Concave
iv. In quadrilateral ABCD, ∠D = 40°, ∠C = 80°, AP bisects angle A and BP bisects angle ∠B; then ∠APB is equal:
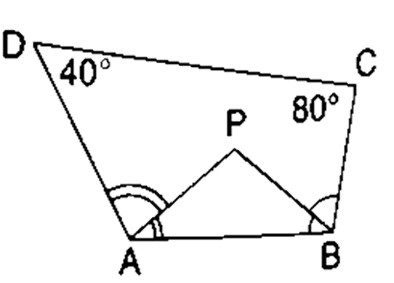
Step 1:Sum of interior angles of a quadrilateral is:
\[
360^\circ
\]Step 2:Given:
\[
\angle D = 40^\circ,\quad \angle C = 80^\circ
\]So,
\[
\angle A + \angle B = 360^\circ – (40^\circ + 80^\circ)\\
\angle A + \angle B = 360^\circ – 120^\circ = 240^\circ
\]Step 3:AP bisects ∠A and BP bisects ∠B.
So,
\[
\angle PAB = \frac{\angle A}{2}, \quad \angle PBA = \frac{\angle B}{2}
\]Step 4:In triangle APB, sum of angles is 180°:
\[
\angle APB + \frac{\angle A}{2} + \frac{\angle B}{2} = 180^\circ\\
\angle APB + \frac{\angle A + \angle B}{2} = 180^\circ
\]Step 5:Substitute \(\angle A + \angle B = 240^\circ\):
\[
\angle APB + \frac{240^\circ}{2} = 180^\circ\\
\angle APB + 120^\circ = 180^\circ\\
\angle APB = 60^\circ
\]Answer: d. 60°
v. The sum of interior angles of a polygon is 900°. The number of sides in this polygon is:
Step 1: Formula for sum of interior angles of a polygon with \( n \) sides is:
\[
(n – 2) \times 180^\circ = 900^\circ
\]Step 2: Solve for \( n \):
\[
(n – 2) = \frac{900^\circ}{180^\circ} = 5\\
n = 5 + 2 = 7
\]Answer: b. 7
Q2: Calculate the sum of angles of a polygon with 10 sides.
Step 1: Recall the formula for the sum of interior angles of a polygon with \( n \) sides:
\[
\text{Sum of interior angles} = (n – 2) \times 180^\circ
\]Step 2: Substitute \( n = 10 \) into the formula:
\[
\text{Sum} = (10 – 2) \times 180^\circ
\]Step 3: Simplify the expression:
\[
= 8 \times 180^\circ = 1440^\circ
\]Answer: The sum of interior angles of a polygon with 10 sides is 1440°.
Q3: Find the number of sides in a polygon if the sum of its interior angles is 16 right angles.
Step 1: Recall that 1 right angle = \(90^\circ\).
So, 16 right angles = \(16 \times 90^\circ = 1440^\circ\).
Step 2: Use the formula for sum of interior angles of a polygon with \( n \) sides:
\[
(n – 2) \times 180^\circ = 1440^\circ
\]Step 3: Solve for \( n \):
\[
n – 2 = \frac{1440^\circ}{180^\circ} = 8\\
n = 8 + 2 = 10
\]Answer: The polygon has 10 sides.
Q4: Is it possible to have a polygon whose sum of interior angles is:
i. 870°
Step 1: Use the formula for sum of interior angles of a polygon with \( n \) sides:
\[
(n – 2) \times 180^\circ = 870^\circ
\]Step 2: Solve for \( n \):
\[
n – 2 = \frac{870^\circ}{180^\circ} = 4.83\ldots
\]Step 3: Since \( n \) is not an integer, a polygon cannot have sum of interior angles 870°.
Answer: Not possible.
ii. 2340°
Step 1: Use the formula:
\[
(n – 2) \times 180^\circ = 2340^\circ
\]Step 2: Solve for \( n \):
\[
n – 2 = \frac{2340^\circ}{180^\circ} = 13\\
n = 13 + 2 = 15
\]Step 3: Since \( n \) is an integer, a polygon with 15 sides can have sum of interior angles 2340°.
Answer: Possible (15-sided polygon).
iii. 7 right angles
Step 1: Convert right angles to degrees:
\[
7 \times 90^\circ = 630^\circ
\]Step 2: Use the formula:
\[
(n – 2) \times 180^\circ = 630^\circ
\]Step 3: Solve for \( n \):
\[
n – 2 = \frac{630^\circ}{180^\circ} = 3.5
\]Step 4: Since \( n \) is not an integer, such a polygon is not possible.
Answer: Not possible.
Q5:
i. If all the angles of a hexagon are equal, find the measure of each angle.
Step 1: The sum of interior angles of a polygon with \( n \) sides is:
\[
(n – 2) \times 180^\circ
\]Step 2: For a hexagon, \( n = 6 \). So, sum of interior angles:
\[
(6 – 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ
\]Step 3: Since all angles are equal, each angle is:
\[
\frac{720^\circ}{6} = 120^\circ
\]Answer: Each angle of the hexagon measures 120°.
ii. If all the angles of a 14-sided figure are equal, find the measure of each angle.
Step 1: Use the formula for sum of interior angles:
\[
(n – 2) \times 180^\circ
\]Step 2: For \( n = 14 \):
\[
(14 – 2) \times 180^\circ = 12 \times 180^\circ = 2160^\circ
\]Step 3: Since all angles are equal, each angle is:
\[
\frac{2160^\circ}{14} = \frac{1080^\circ}{7} = 154\frac{2}{7}^\circ
\]Answer: Each angle of the 14-sided figure measures approximately \(154\frac{2}{7}^\circ\).
Q6: Find the sum of exterior angles obtained on producing the sides of a polygon, in order, with 7 sides.
Step 1: The sum of exterior angles of any polygon, when taken one at each vertex, is always \(360^\circ\), irrespective of the number of sides.
Step 2: Therefore, for a polygon with 7 sides, the sum of the exterior angles is: \(360^\circ\)
Answer: The sum of exterior angles of a 7-sided polygon is 360°.
Q7: The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are \( (6x – 1)^\circ \), \( (10x + 2)^\circ \), \( (8x + 2)^\circ \), \( (9x – 3)^\circ \), \( (5x + 4)^\circ \), and \( (12x + 6)^\circ \), find each exterior angle.
Step 1: The sum of exterior angles of any polygon is always \( 360^\circ \). So,
\[
(6x – 1) + (10x + 2) + (8x + 2) + (9x – 3) + (5x + 4) + (12x + 6) = 360
\]Step 2: Combine like terms:
\[
6x + 10x + 8x + 9x + 5x + 12x + (-1 + 2 + 2 – 3 + 4 + 6) = 360\\
(6 + 10 + 8 + 9 + 5 + 12)x + ( -1 + 2 + 2 – 3 + 4 + 6 ) = 360\\
50x + 10 = 360
\]Step 3: Solve for \( x \):
\[
50x = 360 – 10 = 350\\
x = \frac{350}{50} = 7
\]Step 4: Find each exterior angle by substituting \( x = 7 \) into the expressions:
\[
6x – 1 = 6 \times 7 – 1 = 42 – 1 = 41^\circ\\
10x + 2 = 10 \times 7 + 2 = 70 + 2 = 72^\circ\\
8x + 2 = 8 \times 7 + 2 = 56 + 2 = 58^\circ\\
9x – 3 = 9 \times 7 – 3 = 63 – 3 = 60^\circ\\
5x + 4 = 5 \times 7 + 4 = 35 + 4 = 39^\circ\\
12x + 6 = 12 \times 7 + 6 = 84 + 6 = 90^\circ
\]Answer: The exterior angles are 41°, 72°, 58°, 60°, 39°, and 90° respectively.
Q8: The interior angles of a pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Find each angle of the pentagon.
Step 1: Let the common ratio be \( k \). Then the angles are \( 4k, 5k, 6k, 7k, \) and \( 5k \).
Step 2: Sum of interior angles of a pentagon with \( n = 5 \) sides is:
\[
(5 – 2) \times 180^\circ = 3 \times 180^\circ = 540^\circ
\]Step 3: Sum of the angles in terms of \( k \):
\[
4k + 5k + 6k + 7k + 5k = 27k
\]Step 4: Equate sum of angles to 540°:
\[
27k = 540^\circ
\]Step 5: Solve for \( k \):
\[
k = \frac{540^\circ}{27} = 20^\circ
\]Step 6: Find each angle:
\[
4k = 4 \times 20^\circ = 80^\circ\\
5k = 5 \times 20^\circ = 100^\circ\\
6k = 6 \times 20^\circ = 120^\circ\\
7k = 7 \times 20^\circ = 140^\circ\\
5k = 5 \times 20^\circ = 100^\circ
\]Answer: The interior angles of the pentagon are 80°, 100°, 120°, 140°, and 100° respectively.
Q9: Two angles of a hexagon are 120° and 160°. If the remaining four angles are equal, find each equal angle.
Step 1: The sum of interior angles of a hexagon (\( n = 6 \)) is:
\[
(6 – 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ
\]Step 2: Let each of the remaining four equal angles be \( x \) degrees. Then:
\[
120^\circ + 160^\circ + 4x = 720^\circ
\]Step 3: Simplify and solve for \( x \):
\[
280^\circ + 4x = 720^\circ\\
4x = 720^\circ – 280^\circ = 440^\circ\\
x = \frac{440^\circ}{4} = 110^\circ
\]Answer: Each of the four equal angles measures 110°.
Q10: The figure given below shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B : ∠C : ∠D = 5 : 6 : 7.

i. Using formula, find the sum of interior angles of the pentagon
Step 1:Formula for sum of interior angles of a polygon with n sides:
\[
(n – 2) \times 180^\circ
\]Step 2:Here, number of sides \(n = 5\).
\[
\text{Sum of interior angles}
= (5 – 2) \times 180^\circ\\
= 3 \times 180^\circ\\
= 540^\circ
\]Answer: Sum of interior angles of the pentagon = 540°
ii. Write the value of ∠A + ∠E
Step 1:Since AB ∥ ED, angles ∠A and ∠E are interior angles on the same side of a transversal.
Step 2:Interior angles on the same side of parallel lines are supplementary.
\[
\angle A + \angle E = 180^\circ
\]Answer: ∠A + ∠E = 180°
iii. Find angles B, C and D
Step 1:Sum of all interior angles of pentagon = 540°.
\[
\angle A + \angle B + \angle C + \angle D + \angle E = 540^\circ
\]Step 2:From part (ii):
\[
\angle A + \angle E = 180^\circ
\]So,
\[
\angle B + \angle C + \angle D = 540^\circ – 180^\circ\\
= 360^\circ
\]Step 3:Given ratio:
\[
\angle B : \angle C : \angle D = 5 : 6 : 7
\]Let:
\[
\angle B = 5x,\quad \angle C = 6x,\quad \angle D = 7x
\]Step 4:
\[
5x + 6x + 7x = 360^\circ\\
18x = 360^\circ\\
x = 20^\circ
\]Step 5:
\[
\angle B = 5 \times 20^\circ = 100^\circ\\
\angle C = 6 \times 20^\circ = 120^\circ\\
\angle D = 7 \times 20^\circ = 140^\circ
\]Answer: ∠B = 100°, ∠C = 120°, ∠D = 140°
Q11: Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.
Step 1: Let the polygon have \( n \) sides. Then, it has 2 right angles and \( n – 2 \) angles of 120° each.
Step 2: The sum of interior angles of the polygon is:
\[
2 \times 90^\circ + (n – 2) \times 120^\circ
\]Step 3: Use the formula for the sum of interior angles:
\[
(n – 2) \times 180^\circ = 2 \times 90^\circ + (n – 2) \times 120^\circ
\]Step 4: Simplify the equation:
\[
180n – 360 = 180 + 120n – 240\\
180n – 360 = 120n – 60
\]Step 5: Bring all terms to one side:
\[
180n – 360 – 120n + 60 = 0\\
60n – 300 = 0
\]Step 6: Solve for \( n \):
\[
60n = 300\\
n = \frac{300}{60} = 5
\]Answer: The polygon has 5 sides.
Q12: In a hexagon ABCDEF, side AB is parallel to side FE and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3. Find ∠B and ∠D.
Step 1: Calculate the sum of all interior angles of the hexagon.
Sum of angles = (n – 2) * 180°
For a hexagon, n = 6
Sum = (6 – 2) * 180° = 4 * 180° = 720°
∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°
Step 2: Use the property of parallel sides.
Since AB || FE, the sum of co-interior angles ∠A and ∠F is 180°.
∠A + ∠F = 180°
Step 3: Find the sum of the remaining angles.
∠B + ∠C + ∠D + ∠E = 720° – (∠A + ∠F)
∠B + ∠C + ∠D + ∠E = 720° – 180° = 540°
Step 4: Use the given ratio to find the angles.
Let the angles be 6k, 4k, 2k, and 3k.
6k + 4k + 2k + 3k = 540°
15k = 540°
k = 540° / 15 = 36°
Step 5: Calculate specific angles.
∠B = 6k = 6 * 36° = 216°
∠D = 2k = 2 * 36° = 72°
Answer: ∠B = 216° and ∠D = 72°.
Q13: The angles of a hexagon are \( x + 10^\circ \), \( 2x + 20^\circ \), \( 2x – 20^\circ \), \( 3x – 50^\circ \), \( x + 40^\circ \), and \( x + 20^\circ \). Find \( x \).
Step 1: The sum of interior angles of a hexagon (\( n=6 \)) is:
\[
(6 – 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ
\]Step 2: Sum of all given angles:
\[
(x + 10) + (2x + 20) + (2x – 20) + (3x – 50) + (x + 40) + (x + 20) = 720
\]Step 3: Combine like terms:
\[
x + 2x + 2x + 3x + x + x + 10 + 20 – 20 – 50 + 40 + 20 = 720\\
(1 + 2 + 2 + 3 + 1 + 1)x + (10 + 20 – 20 – 50 + 40 + 20) = 720\\
10x + 20 = 720
\]Step 4: Solve for \( x \):
\[
10x = 720 – 20 = 700\\
x = \frac{700}{10} = 70
\]Answer: The value of \( x \) is 70.
Q14: In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3 : 7. Find the biggest angle of the pentagon.
Step 1: Sum of interior angles of a pentagon (\( n = 5 \)) is:
\[
(5 – 2) \times 180^\circ = 3 \times 180^\circ = 540^\circ
\]Step 2: Let the three remaining angles be \( k \), \( 3k \), and \( 7k \). Their sum is:
\[
k + 3k + 7k = 11k
\]Step 3: The sum of all angles:
\[
40^\circ + 60^\circ + 11k = 540^\circ
\]Step 4: Solve for \( k \):
\[
100^\circ + 11k = 540^\circ\\
11k = 540^\circ – 100^\circ = 440^\circ\\
k = \frac{440^\circ}{11} = 40^\circ
\]Step 5: Find the three remaining angles:
\[
k = 40^\circ, \quad 3k = 120^\circ, \quad 7k = 280^\circ
\]Step 6: Identify the biggest angle:
\[
\max(40^\circ, 60^\circ, 40^\circ, 120^\circ, 280^\circ) = 280^\circ
\]Answer: The biggest angle of the pentagon is 280°.



Leave a Comment