Introduction
In everyday life, we use integers when we go for shopping, banks, to measure any quantity etc. Integers are everywhere! They play an important role in our life. It represents the set of all negative numbers and whole numbers.
Integers
It is the set of numbers which include all positive numbers, zero and all negative numbers.
It is represented as- \({……,-3,-2,-1,0,1,2,3,…..}\)
- \(1,2,3,… \) are called positive integers or non-negative integers.
- \(-1,-2,-3,….\) are called negative integers or non-positive integers.
- \(0\) is an integer which is neither positive nor negative.
- Integers doesn’t have any decimal or fractional part.
- Decimal Numbers are not integers.
What is the need of negative numbers or integers?
Any number either positive or negative is used to represent any quantity or value. There were many real-world problems which were not defined, before the invention of negative numbers. Brahmagupta, an Indian mathematician in seventh century is said to be the first to write rules for negative numbers.
Negative numbers represent all values that goes below zero.
Now, let us understand the need of negative numbers with real life example:
- Temperature and Elevation: To represent temperatures below zero and elevations below sea level, negative numbers are used.
- Balance and Debts: In accounting and finance, negative numbers are used to represent debts or withdrawals.
- Mathematical Operations: Subtraction of a larger number from a smaller number gives negative number.
- Quiz or Exams: For every wrong answer, some negative value is deducted from the result.
- Games: Different games or sports use negative numbers when counting the scores/points or for giving a penalty.
How to represent integers on number line?
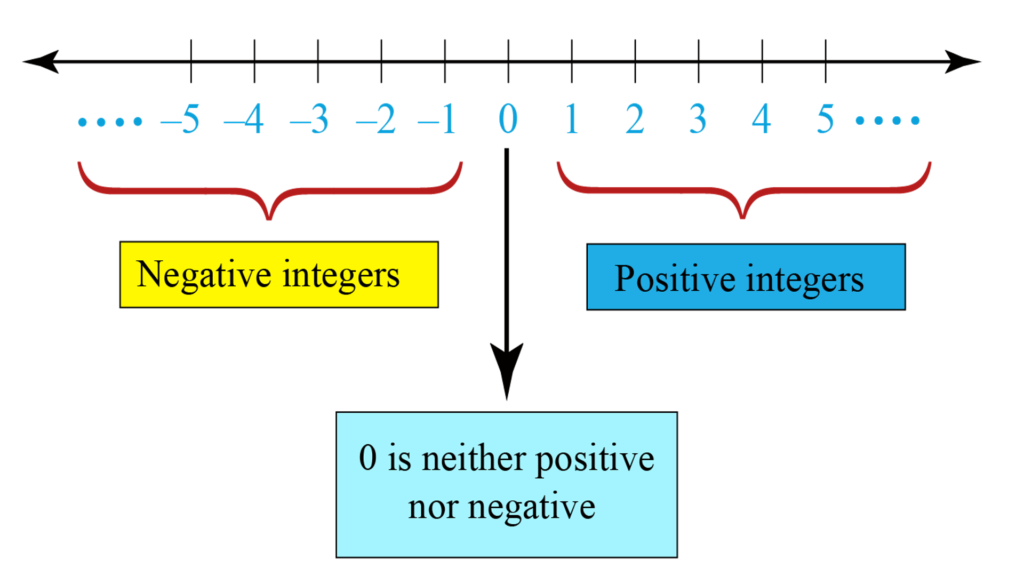
- Step1: Draw straight line. At the centre of the line, mark a point and name it as \(0\).
- Step 2: Mark multiple points on left and right side of \(0\).
- Step 3: On right side of \(0\), label the points as positive integers \((1,2,3,…)\). On left side of \(0\), label the points as negative integers \((-1,-2,-3,…)\).
- Step 4: Put arrows at the two ends of number line, which means that it can be extended indefinitely in both the directions.
Comparison of integers
- When both integers are positive: To compare both positive integers, the one with larger value is greater.
Example: \(7 > 5\) - When one integer is positive and other is negative: Positive integer is always greater than negative integer.
Example: \(9 >-85\) - When both integers are negative: To compare both negative integers, the one with smaller value is greater.
Example: \(-2 >-8\) - On number line: Any integer occurring on the right is always greater than that occurring on left.
What is absolute value of an integer?
It is the numerical value of an integer, regardless of sign.
Example: \(|-2| = |2| , |2| = |2|\)
Operations on Integers
1. Addition
Combining two integers to get integer. There are some rules for integer addition:
- Rule 1: Addition of two positive integers is always a positive integer.
Example: \(10+2=12\) - Rule 2: Addition of two negative integers is always a negative integer. Sum is obtained by adding numerical values of both negative integers and negative sign is placed before it.
Example: \((-5) + (-2) = -(5+2) = -7\) - Rule 3: To add one positive and one negative integer, calculate the difference between their numerical value and put sign of that integer which has greater numerical value.
Example: \(6 + (-8) = (-8) + 6 = -(8-6) = -2\)
Properties of addition of integers:
a) Closure Property: It says that addition of any two integers is always a integer.
Closure property is stated as:
\((x+y) ∈ I\) , where \(x,y ∈ I, I\) is set of integers.
Example 1: \(2+5 =7\)
Example 2: \(4+ (-7) = -3\)
Both \(7\) and \(-3\) are integers.
b) Associative Property: The sum of any three integers remains same regardless of how they are placed.
Associative property is stated as:
\((x+y)+z = x+(y+z)\) ,where \(x,y,z ∈ I, I\) is set of integers.
Example 1: \((8+2) +(-3) = 8+(2-3)\)
By solving, \(10-3 = 8-1\)
\(7=7\)
Example 2: \([ (-7)+ (-3) ] + (-4) = (-7) + [ (-3) + (-4) ]\)
By solving, \((-10) + (-4) = (-7) + (-7)\)
\(-14 = -14\)
c) Commutative Property: This property states that sum of two integers remains same regardless the order.
Commutative Property is stated as:
\(x+y=y+x\), where \(x,y ∈ I, I\) is set of whole numbers.
Example 1: \((-4) + 3 = 3 + (-4)\)
By solving, \(-1=-1\)
Example 2: \((-15) + (-5) = (-5) + (-15)\)
By solving, \(-20 = -20\)
d) Additive Identity: In integers, 0 is the additive identity.
\(x+0 = 0+x\), for every integer x.
Example: \((7+0) = (0+7)\)
\(7=7\)
e) Additive Inverse: For integer x, there is another integer (-x), which is additive inverse.
\((x) + (-x) = (-x) + (x) = 0\)
Example: \(5 + (-5) = (-5) + 5 =0\)
2. Subtraction
To subtract any two integers, follow same-change-change rule.
Same-change-change rule: Keep the first integer with same sign, change subtraction sign to addition and then change the sign of second integer.
Example 1: \(27- (-5) = 27 + 5 = 32\)
Example 2: \(-2- (-4) = -2 + 4 = 2\)
So, \(a-b = a + (-b)\) or \(= a +\) (additive inverse of \(b\)), where \(a\) and \(b\) are integers.
Properties of Subtraction of integers:
a) Closure Property: It says that difference of two integers is always integer.
Closure property is stated as:
\((x-y) ∈ I\), where \(x,y ∈ I\), I is set of integers.
Example 1: \(2-5 = -3\)
Example 2: \(4- (-2) = 6\)
Both \(-3\) and \(6\) are integers.
b) Additive Inverse: For integer -x, there is another integer x, which is additive inverse.
\((-x) + (x) = (x) + (-x) = 0\)
Example: \((-4) + 4 = 4 + (-4) =0\)
3. Multiplication
Product of two integers to get integer. There are some rules for integer multiplication:
- Rule 1 : Multiplication of two same sign integers is always a positive integer.
\((+ve)\times(+ve)\ =\ +ve\)
\((-ve)\times(-ve)\ =\ +ve\)
Example: \(10\times2=20,\ \ (-3)\times(-2)=6\) - Rule 2: Multiplication of one positive integer with one negative integer is always a negative integer.
\((+ve)\times(-ve)\ =\ -ve\)
\((-ve)\times(+ve)\ =\ -ve\)
Example: \((-5)\times(2)\ =\ (-10)\ ,\ 6\times(-3)=\ (-18)\)
| First Integer | Second Integer | Result |
| +ve | +ve | +ve |
| +ve | -ve | -ve |
| -ve | +ve | -ve |
| -ve | -ve | +ve |
Properties of Multiplication of integers:
a) Closure Property: It says that multiplication of any two integers is always a integer.
Closure property is stated as:
\((x\times\ y)\ =\ xy\ ,\ xy\in\ I\) , where \(x,y\ \in\ I,\ I\) is set of integers.
Example 1: \(3\times5\ =15\)
Example 2: \(4\times\ (-6)\ =\ -24\)
Both \(15\) and \(-24\) are integers.
b) Associative Property: The product of any three integers remains same regardless of how they are placed.
Associative property is stated as:
\(x\times(y\times\ z)=\ (x\times\ y)\times\ z\) ,where \(x,y,z\ \in\ I,\ I\) is set of integers.
Example 1: \(8\times(5\times2)\ =\ (8\times5)\times2\)
By solving, \(8\times10\ =\ 40\times2\)
\(80=80\)
Example 2: \((-7)\times[(-3)\times(-4)]=[(-7)×(-3)]×(-4) \)
By solving, \((-7)\times(12)=(21)\times(-4) \)
\(-84\ =\ -84\)
c) Commutative Property: This property states that multiplication of two integers remains same regardless the order.
Commutative Property is stated as:
\(x\times\ y=y\times\ x\), where \(x,y\ \in\ I,\ I\) is set of whole numbers.
Example 1: \((-4)\times3\ =\ 3\times(-4)\)
By solving, \(-12=-12\)
Example 2: \((-15)\times(-2)=(-2)\times(-15)\)
By solving, \(30\ =\ 30\)
d) Multiplicative Identity: Integer 1 is multiplicative identity.
For every integer \(x,\ x\times1\ =\ 1\times\ x\),
Example: \((-4)\times1=1\times(-4)\)
\(-4=-4\)
e) Multiplicative Inverse: For integer x, there is another integer (), which is multiplicative inverse.
\(\left(\frac{1}{x}\right)\), which is multiplicative inverse.
\((x)\times\left(\frac{1}{x}\right)=1\)
Example: \(3\times\left(\frac{1}{3}\right)=1\)
f) Distributive Property: It states that multiplication is distributive over addition and subtraction.
\(x\times(y+z)=x\times\ y+x\times\ z\) where \(x,y,z\ \in\ I,\ I\) is set of whole numbers.
Example 1: \((-4)\times(-3+2)=(-4\times-3)+(-4\times2)\)
By solving, \((-4)\times(-1)=12+(-8)\)
\(4=4\)
Example 2: \(2\times(13-10)=(2\times13)-(2\times10)\)
By solving, \(2\times3=26-20\)
\(6=6\)
4. Division
Division of two integers gives integer. Number to be divided is dividend. Number which divides any given number is called divisor. Result of division is quotient.
\(\frac{Dividend}{Divisor}=Quotient\)
There are some rules for integer division:
- Rule 1 : Division of two same sign integers is always a positive integer.
\((+ve)\div(+ve)=+ve\)
\((-ve)\div(-ve)=+ve\)
Example: \(10\div2=5,\ \ (-9)\div(-3)\ =\ 3\) - Rule 2: Division of one positive integer with one negative integer is always a negative integer.
\((+ve)\div(-ve)=-ve\)
\((-ve)\div(+ve)=-ve\)
Example: \((-8)\div(2)=(-4),\ \ 6\div(-3)=(-2)\)
Properties of Division of integers:
- Division of integers does not satisfy closure, commutative, associative, distributive, identity for division and division inverse.
- For every non-zero integer \(x,\ 0\ \div\ x\ =0\).
- For every integer \(x,\ x\ \div\ 0\) is not defined.
How to solve any expression?
In order to solve any expression, the order of operations matters. Order in which operations are performed is:
DMAS (Division, Multiplication, Addition, Subtraction)
If the expression also has brackets, then it must be solved in following sequence:
- Vinculum or bar –
- Round brackets ( )
- Curly brackets { }
- Square brackets [ ]
Note: While removing the brackets, operations within brackets are performed before operations outside it.
Example: \(35-{15+14-\left(13+\bar{2-1+3}\right)}\)
\(35-{15+14-\left(13+4\right)}\) (Removing bar)
\(35-{15+14-17}\) (Removing round bracket)
\(35-12\) (Removing curly bracket)
\(23\)
Successor and Predecessor of integers
Successor of any integer is obtained by adding 1 to the integer.
\(x= x+1\)
Example: Successor of \(45= (45+1) = 46\)
Successor of \(-4= (-4+1) = -3\)
Predecessor of integer is obtained by subtracting 1 from the integer.
\(x= x-1\)
Example: Predecessor of \(45= (45-1) = 44\)
Predecessor of \(-4= (-4-1) = -5\)





Leave a Comment